Proszę o Pomoc :((( moniś92: Proszę o Pomoc Potrzebuję rozwiązania do tych zadań. Uczęszczam do szkoły policealnej i nie mam o tych rzeczach bladego pojęcia Zad.1Rozwiąż równanie log₂x * log_x4 = 2. Zad.2 Dla jakich a dziedziną funkcji y = √ax² + x + a jest zbiór wszystkich liczb rzeczywistych ?

	n		n		n 2
Zad.3 Rozwiąż równanie n +		+		+ ... =		=> Odp. n=5
	2		4

Zad. 4 Oblicz stosunek objętości kuli opisanej na walcu którego przekrój osiowy jest kwadratem, do objętości kuli wpisanej w ten walec. => Odp: 2√2 Zad. 5 Trapez równoramienny ma podstawy a i 4a. Jakiej długości ma być wysokość trapezu, aby w ten trapez można było wpisać okrąg. => Odp. h=2a

ZKS: 1. Ustal dziedzinę i jeżeli nic nie widać to proponuję podstawić za

	2		2
log2x = t czyli logx4 = 2logx2 =		=		.
	log2x		t

ZKS: 2. a > 0 ∧ Δ < 0

krystek:

	log24
1)log2x*		=2 i teraz dla wszystkich x>0 bo D=R+
	log2x

krystek: 2)ax²+x+a≥0 i jest spełnione gdy a≠0 i Δ≤0 lub a=0 i wówczas x≥0

ZKS: 3. Po lewej stronie mamy sumę nieskończonego ciągu geometrycznego a po prawej symbol Newtona.

	1
q =		aby była suma nieskończonego ciągu geometrycznego to |q| < 1 suma wyraża się
	2

wzorem:

	a1
Sn =
	1 − q

natomiast symbol Newtona:

n k		n!
	=
		k!(n − k)!

krystek: przepraszam a>0 miało być i wówczas x≥0 musiałyby być.

ZKS: krystek ma być dla wszystkich liczb rzeczywistych więc warunek a = 0 odpada ponieważ x musi być wtedy większy bądź równy 0 czyli nie jest spełnione dla wszystkich liczb ale Δ ≤ 0 rzeczywiście w porządku ponieważ nie mamy mianownika. Więc a > 0 ∧ Δ ≤ 0. Co do pierwszego to dziedzina to 0 < x ≠ 1.

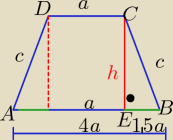
A ku ku: Z warunku wpisania okręgu w trapez: 4a+a= c+c ⇒ 5a=2c ⇒c= 2,5a

	4a−a
|EB|=		= 1,5 a
	2

z tw. Pitagorasa w ΔEBC h²= (2,5a)²− (1,5a)² ⇒ h²= 6,25a²−2,25a² ⇒h²= 4a² ⇒ h= 2a

moniś92: Do tej pory zrozumiałam tylko wyjaśnienie A ku ku. Wszystko czarno na białym nad pozostałymi nadal główkuję ale ciężko mi to idzie

A ku ku:

	a		a√2
r =		R=
	2		2

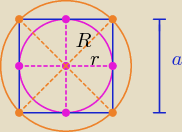
	4		4
V(kuli wpisanej) =		πr2 V (kuli opisanej) =		πR3
	3		3

V(opisanej)		4   πR3 3		R3
	=		=		=
V(wpiranej)		4   πr3 3		r3

	a3(√2)3   23		2√2		1
=		=		*		= 2√2
	a3   23		8		8

krystek: zad 2 Masz wyrażenie pod pierwiastkiem o ono musi być ≥0 A ma ono postać ax²+x+a więc mamy ax²+x+a≥0 Tera ta nierówność ma być spełniona dla wszystkich x−ów Czyli a>0 i Δ≤0 Liczysz Δ: Δ=b²−4ac=1−4a² 1−4a²≤0⇔(1+2a)(1₂a)≤0

A ku ku: Poprawiam zapis ostatniego ułamka piętrowego tak:

	a3(√2)3		23
		*		= ..... upraszczasz a3 i 23
	23		a3

zostaje (√2)³= √2*√2*√2= 2√2