<beczy>
Ilonka: Liczba punktów wspólnych okręgu o równaniu (x−1)√2+y√2=4 z prostą o równaniu y=−1 jest
równa? Nie mam pojęcia jak to wyliczyć..
16 lut 19:44
Ilonka: sory strzeliłam gafe(x−1)2+y2=4
16 lut 19:45
Aga1: Narysuj sobie okrąg o środku S=(1,0) i promieniu 2
i prostą równoległą do osi x, przechodzącą przez punkt (0,−1)
I zobacz w ilu punktach ta prosta przecina okrąg.
16 lut 19:48
konrad: może też obliczyć

16 lut 19:49
konrad: *możesz
16 lut 19:49
Ilonka: juz rysuje.. zobaczę co z tego mi wyjdzie
16 lut 19:50
Ilonka: mogłabym ale nawet nie wiem jak się za to zabrać
16 lut 19:51
Ilonka: nic nie wychodzi

16 lut 19:54
konrad: nie umiesz narysować okręgu o zadanym środku i promieniu?
16 lut 19:55
konrad: ani prostej ?
16 lut 19:55
Ilonka: no rysunek mam
16 lut 19:57
konrad: no i co wyszło?
16 lut 19:57
A ku ku:
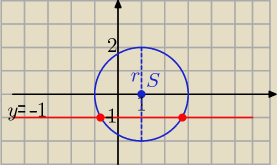
r=2 S(1,0)
16 lut 20:02
Ilonka: rysunek hehe
16 lut 20:04
konrad: no to ile ma punktów wspólnych

16 lut 20:05
A ku ku:
Ładny?

16 lut 20:06
Ilonka: a mozna to wyliczyć tez inaczej?
16 lut 20:06
Ilonka: rysunek jest sliczny

16 lut 20:07
konrad: można
podstawiasz do równania okręgu pod igreka −1 i liczysz x i tyle ile będzie rozwiązań, tyle jest
punktów
16 lut 20:08
A ku ku:
Algebraicznie: y= −1
to (x−1)2+(−1)2= 4 ⇒ (x−1)2= 3 ⇒ x−1= √3 lub x−1= −√3
x= 1+√3 lub x= 1−√3
są dwa takie punkty wspólne tej prostej i okręgu
P1( 1+√3, −1) i P2(1−√3, −1)
16 lut 20:16
Ilonka: dzięki śliczne ale i tak nierozumiem co i jak.. mam nadzieje, ze takie zadanie na maturze mi
sie nie trafi

16 lut 20:23
A ku ku:
Jeżeli to zadanie "zamknięte" ......... to tylko z rysunku i jest bardzo łatwe

16 lut 20:24
konrad: do obliczenia też jest bardzo łatwe

16 lut 20:30


 r=2 S(1,0)
r=2 S(1,0)





