zadania Skylar: mam tu kilka zadań, których nie umiem rozwiązać Pomożesz? 1. Kąt BAC trójkąta ABC ma miarę 13 ^o, a kąt ACB MIARĘ 119 ^o. wysokość CD dzieli bok AB na dwa odcinki, z których krótszy ma długość 25 cm. Oblicz długość boku AC. 2. Dwa kąty trójkąta mają miary 30^o i 50^o. Oblicz miarę kąta, jaki tworzy dwusieczna trzeciego kąta z wysokością poprowadzoną z wierzchołka tego kąta. 3. Środkowa poprowadzona z wierzchołka kąta ostrego równoramiennego trójkąta prostokątnego ma długość 5. Oblicz pole tego trójkąta. 4.Kąt między ramionami trójkąta równoramiennego ma miarę 40 ^o. Promień okręgu wpisanego w ten trójkąt ma długośc 2,1 cm. Oblicz długość podstawy trójkąta. 5. Jeden z kątów trójkąta prostokątnego ma miarę 60^o, a promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta. 6. Ramię trójkąta równoramiennego ma długość √3 , a kąt przy podstawie ma miarę 30 ^o. Okrąg o jest styczny do prostej zawierających jedno z ramion, a drugie ramię jest jego cięciwą. Oblicz długości odcinków, na jakie okrąg o dzieli podstawę trójkąta. 7.Dwusieczna kąta prostego trójkąta prostokątnego dzieli przeciwprostokątną na odcinki o długościach a i b. oblicz długość przyprostokątnych tego trójkąta.

Aga1: Zad.3 Środkowa w trójkącie prostokątnym poprowadzona z wierzchołka kąta prostego jest równa połowie przeciwprostokątnej c=2*5=10 W trójkącie prostokątnym równoramiennym przyprostokątne są równe a .Z Pitagorasa a² +a²=c² Lub c=a√2 P={a²}{2}

Skylar: up

wmboczek: Zad 7. (a+b)²=k²a²+k²b² k − wsp proporcjonalności z tw o dwusiecznej k=? boki mają długość ak i bk

wmboczek: Zad 1. AC=25/sin13

Skylar: dziękuję Wam, a pomoże mi ktoś jeszcze z pozostałymi?

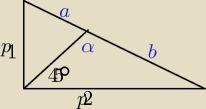ejendi: 7.Dwusieczna kąta prostego trójkąta prostokątnego dzieli przeciwprostokątną na odcinki o długościach a i b. oblicz długość przyprostokątnych tego trójkąta. p1,p2 przyprostokątne b/sin45=p2/sinα a/sin45=p1/sin(180−α)=p1/sinα 1.p1²+p2²=(a+b)² 2.p1=a√2sinα 3.p2=b√2sinα 2 i 3 wstawiamy do1

	(a+b)2
to sinα=√
	2(a2+b2