może ktoś pomóc blizniak: punkty A(2;3) B(2;4) C(4;6) to wierzchołki trójkąta oblicz obwód trójkąta ABC

katie :): musisz obliczyc odleglosci mieszy poszczegolnymi punktami √(x₁ −x₂)²+(y₁ −y₂)²

paula:

madzia:

Nikka:

	1
P =		|AC|*|BD|
	2

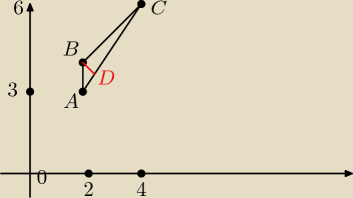
|AC| = √(x_C−x_A)²+(y_C−y_A)² |AC| = √(4−2)²+(6−3)² |AC| = √4+9 |AC| = √13 |BD| = ? Wyznaczmy równanie prostej AC: y = ax + b

	3
A, C ∊ pr. AC → 3 = 2a + b i 6 = 4a + b → a =		, b = 0
	2

	3
pr. AC: y =		x
	2

Niech prosta BD ma postać: y = cx + d. Punkt D należy do prostej BD prostopadłej do prostej AC.

	3		2		2
Skoro pr. AC⊥ pr. BD to c*(		) = −1 → c = −		→ y = −		x + d
	2		3		3

	2		16
Punkt B∊pr. BD czyli 4 = −		*2 + d → d =
	3		3

	2		16
pr. BD: y = −		x +
	3		3

Punkt D jest punktem przecięcia prostych AC i BD:

	2		16
y = −		x +
	3		3

	3
y =		x
	2

	32		48
Stąd x =		, y =
	13		13

Oblicz długość odcinka BD i podstaw do wzoru na pole trójkąta... (sprawdź obliczenia).

Nikka: no to się uśmiałam sama z siebie − bo to obwód trzeba było policzyć, a nie pole jak obwód to tak jak napisała Katie − trzeba obliczyć długości boków (odległości między wierzchołkami Δ−a)

123: Zrobiłaś kawał dobrej, nikomu niepotrzebnej roboty

Nikka: praktyka czyni mistrza nio, ale fakt niepotrzebnie się napisałam