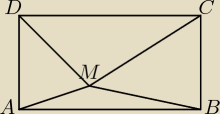
dowód z planimetrii Środa: Udowodnij, że |AM|² + |CM|² = |BM|² + |DM|². Jedyny sposób, jaki przychodzi mi do głowy, to wykorzystanie tw. Pitagorasa po poprowadzeniu odcinka równoległego do AD i przechodzącego przez M. Nie wiem tylko, czy to jest dobra metoda. Może ktoś zna inną? Proszę o jakąś podpowiedź.

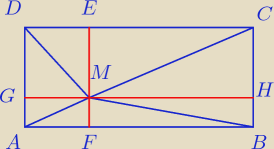
rumpek: metoda dobra, teraz tylko ją odpowiednio wykorzystaj (dodaje rysunek). Odpowiednio ponumeruj proste czerwone, które zaznaczyłem i dalej już łatwo

rumpek: dobra nawet chyba to zrobię z nudów chwilka

rumpek: 1^o

⎧	|GM|2 + |GA|2 = |AM|2
⎨		(dodajemy stronami)
⎩	|MH|2 + |CH|2 = |CM|2

|AM|² + |CM|² = |GM|² + |GA|² + |MH|² + |CH|² 2^o

⎧	|MH|2 + |GA|2 = |BM|2
⎨		(dodajemy stronami)
⎩	|GM|2 + |CH|2 = |DM|2

|BM|² + |DM|² = |MH|² + |GA|² + |GM|² + |CH|² 3^o |AM|² + |CM|² = |BM|² + |DM|² c.n.u.

Środa: Dzięki tak właśnie robiłam, ale nie byłam pewna czy dobrze.