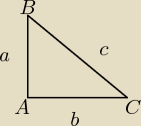
 iloczyn sinusów kątów ostrych pewnego trójkąta prostokątnego jest równy 3/4. Oblicz sumę
cosinusów tych kątów .
sinα * sinβ=3/4
a/b * b/c=3/4 cosα + cosβ=b/c+a/c
a/c=3/4*c/b
b/c+3/4:c/b= b/c +3c/4b= b*4b/c* 4b + 3c*c/c*4b= 4b2 + 3c2/ c*4b
pomocy co dalej mam zrobic? czy to wogole jest dobrze?
iloczyn sinusów kątów ostrych pewnego trójkąta prostokątnego jest równy 3/4. Oblicz sumę
cosinusów tych kątów .
sinα * sinβ=3/4
a/b * b/c=3/4 cosα + cosβ=b/c+a/c
a/c=3/4*c/b
b/c+3/4:c/b= b/c +3c/4b= b*4b/c* 4b + 3c*c/c*4b= 4b2 + 3c2/ c*4b
pomocy co dalej mam zrobic? czy to wogole jest dobrze?
| 3 | b | a | 3 | ab | 3 | |||||||
sinα*sinβ= | ⇒ | * | = | ⇒ | = | ⇒ab=......
| ||||||
| 4 | c | c | 4 | c2 | 4 |
| a+b | |
=?
| |
| c |
| a2+b2 | (a+b)2−2ab | ||
=1 co mozemy zapisac inaczej: | =1 ⇒ | ||
| c2 | c2 |
| (a+b)2 | 2ab | a+b | 2ab | |||||
=1+ | ⇒ ( | )2=1+ | ||||||
| c2 | c2 | c | c2 |
| 10 | ||
(sinα+cosα)2 = sin2 + cos2 + 2sincos = | ||
| 4 |
| 10 | ||
(sinα+cosα)2 = | ||
| 4 |
| √10 | ||
sin + cos = | ||
| 2 |
