.
buhaj: napisz równanie stycznych do okregu
x2+y2−2x+6y+5=0
i prostopadłych do prstej x−2y+2=0
rumpek:
1
o
x
2 + y
2 − 2x + 6y + 5 = 0
(x
2 − 2x + 1) − 1 + (y
2 + 6y + 9) − 9 + 5 = 0
(x − 1)
2 + (y + 3)
2 = 5
S(1,−3) r = √5
2
o
x − 2y + 2 = 0
−2y = −x − 2 / : (−2)
Prostopadła spełnia warunek: a
1 * a
2 = −1
Zatem prostopadła prosta będzie miała y = −2x + b
2x + y − b = 0
3
o
Teraz pozostało obliczyć b, mogę uczynić to na wiele sposobów (jeden z nich to podstawić tę
prostą y = −2x + b pod równanie okręgu, i następnie rozwiązać równanie kwadratowe dla Δ
b = 0)
Ja jednak wybiorę inny sposób − odległość prostej od punktu, mianowicie policzę odległość
prostej y = −2x + b od punktu S(1, −3) (a wiem, że ta odległość wynosi
√5 ), zatem do
dzieła.
d = r
| | |2 * 1 + 1 * (−3) + b| | |
d = |
| |
| | √22 + 12 | |
|b − 1| = 5
b − 1 = 5 ∨ b − 1 = −5
b = 6 ∨ b = − 4
Czyli dwa równania:
y = −2x + 6 ∨ y = −2x − 4
Będzie jak jeżeli się nie pomyliłem




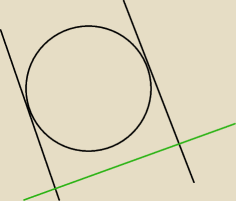 nie wiem czy dobrze rozumiem treść zadania
te dwie czarne styczne mają być prostopadłe do zielonej prostej?
nie wiem czy dobrze rozumiem treść zadania
te dwie czarne styczne mają być prostopadłe do zielonej prostej?
