Da radę obliczyć nie za pomocą wektorów? NICE: Trójkąt o wierzchołkach A=(0,0), B=(1,4), C=(5,2) ma pole? ma wyjść 9. Da się może to zadanie obliczyć jakoś inaczej niż przez wektory?

rumpek: No pewnie, jest taki fajny wzór w tablicach matematycznych.

rumpek:

	1
P =		|(xb − xa)(yc − ya) − (yb − ya)(xc − xa)|
	2

NICE: O super Nie wiedziałam Dzięki wielkie

Mila: Możesz narysować w układzie wsp. obliczyć: 5*4−(0,5*1*4+0,5*5*2+0,5*2*4 )=20−11=9 poziom gimnazjum.

krystek: Wzorem Herona , obliczając długości każdego boku.

krystek: https://matematykaszkolna.pl/strona/503.html

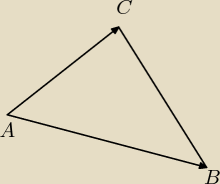Gustlik: Rumpek, ten wzór wywodzi się z wyznacznika wektorów i w tej postaci jest nieprzejrzysty i w dodatku trudny do ogarnięcia tasiemiec. Lepiej wyznacznikiem wektorów to policzyć − w zasadzie ten sam wzór, tylko bardziej obrazowy sposób − wyjaśnienie tej metody tutaj : A=(0,0), B=(1,4), C=(5,2) Liczę współrzędne wektorów AB^→=B−A=[1−0, 4−0]=[1, 4] AC^→=C−A=[5−0, 2−0]=[5, 2] Wyznacznik wektorów: d(AB^→, AC^→)= | 1 4 | | 5 2 | =1*2−4*5=2−20=−18

	1
Pole =		|d(AB→, AC→)|
	2

	1
Pole =		*|−18|=9
	2

Gustlik: Tu wyjaśniam wyznacznikową metodę obliczania pól: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 .