Suma Godzio: Ma ktoś pomysł jak takie coś policzyć:

	b − a		1
limn→∞[		* ∑nk=1		]
	n		k   (a + (b − a))2   n

Artur z miasta Neptuna: 1. liczysz czemu równa jest ta suma 2. mnożysz ze stałą 3. wyliczasz granicę

Trivial: Pan Godzio nie umie takich trywializmów?

Godzio: 1. Ciekawa wskazówka

	1
Potrzebowałem wyliczyć całkę górną z funkcji		na odcinku [a,b] i przyjąłem ciąg
	x2

podziałów

b − a
	, ale teraz zobaczyłem, że jest to bez sensu i mam pytanie, mogę wziąć sobie taki
n

podział: a < aq < aq² < ... < aqⁿ = b gdzie q = ⁿ√^b_a ? To chyba bez różnicy co wezmę hm ?

Trivial: Muszę sobie przypomnieć jak się przybliżało sumę całką. Wtedy zadanie stanie się trywialne.

Godzio: No właśnie nie To nie o to chodzi, bo przejdziesz do czegoś czego masz dowieźć, takiej opcji nie ma (chyba )

Godzio:

	1
Bo to tak jak Ty mówisz, to wyciągasz		z mianownika i już jest wzór pod całkę.
	n2

Trivial: Dowóz nie będzie trudny. Gorzej z dowodem.

Godzio: Chodzi Ci o dowód, że z odpowiedniej granicy można przejść na całkę?

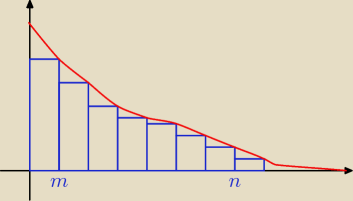
Trivial: Jeżeli f − malejąca to ∫_m...n+1f(x)dx ≤ ∑_k=m..nf(k) ≤ ∫_m−1..nf(x)dx

Godzio:

	1
No tyle wiem, właśnie mam obliczyć tę całkę górną i dolną na [a,b], żeby pokazać, że
	x2

jest całkowalne ...

Trivial: Źle narysowałem rysunek, ale to co. <:

Trivial: Policzyć normalnymi metodami? Czy definicjami?...

Godzio: Definicjami ...

Trivial: Nie wiem jak się liczy całki z definicji...

Godzio: Ehhh chyba będę musiał poczekać do jutrzejszych ćwiczeń Przy moim ciągu podziałów nie wychodzi to co powinno ...

Trivial: Spróbowałem właśnie policzyć... I nawet mi wyszło. Użyłem definicji: ∫_a...b f(x)dx = lim_n→∞ ∑_k=0...n−1 f(x_k)Δx_k W tym konkretnym przypadku...

	1		1
∫a...b		dx = limn→∞ ∑k=0...n−1		Δxk = g
	x2		xk2

Weźmy x_k = aq^k dla k = 0 mamy x₀ = a dla k = n mamy x_n = aqⁿ = b → q = ⁿ√b/a Δx_k = aq^k+1−aq^k = aq^k(q−1).

	1
g = limn→∞ ∑k=0...n−1		aqk(q−1)
	a2q2k

	q−1		1
= limn→∞		∑k=0...n−1
	a		qk

	q−1		1−q−n
= limn→∞		*
	a		1−q−1

	q−1		a   1−   b
= limn→∞		*
	a		q−1   q

	a   1−   b
= limq→1 q *
	a

	1		1
=		−		.
	a		b

To o to chodziło? Pierwsza całka z definicji.

Basia: Godziu możesz przyjąć dowolny sposób podziału odcinka [a,b]. Jedyny warunek jaki musi być spełniony to ten, że przy n→+∞ odcinki, na które dzielisz dążą do 0.

	b−a
Nie zawsze, jak widać na tym przykładzie, podział na równe odcinki o długości		da nam
	n

to co trzeba. To co proponujesz trzeba troszeczkę dopracować, bo ⁿ√b/a zapewne istnieje, nie całkujesz przecież chyba po przedziale, do którego należy 0, ale dla a<b<0 nie zachodzi chyba a<a*q<..... ? Trzeba, albo wiedzieć, albo liczyć na trafny pomysł co tu mogłoby pasować.

Trivial: Czemu nie zachodzi?

Basia: a nie; jednak zachodzi, coś mi się przestawiło a chodzi dokładnie o to co policzyłeś Trivial

Godzio: Znalazłem błąd ... Trivial ponownie mnie uratowałeś Basia dzięki

Trivial:

Godzio:

	b		a
Jak było q−n to mi z tego wyszło		, a powinno		... i w sumie 2 razy robiłem i
	a		b

oba tak samo wyszło i stwierdziłem, że zły podział wziąłem Ale jestem aż z siebie dumny, że wpadłem na taki sposób

Basia: dla obu Panów

Godzio: Zapomniałem dodać, ja miałem to zrobić dla a > 0 więc ... no

Trivial: To za wiele i tak nie pomaga. Wynik wyszedł dla każdego przedziału a<b bez zera.

Basia: a tak nawiasem mówiąc nie możesz po prostu skorzystać z twierdzenia: każda funkcja ciągła na przedziale [a;b] jest na tym przedziale całkowalna i udowodnić tylko ciągłość ? o czym Wy dyskutujecie; wynik Triviala jest dobry

	1		1
∫		dx = −
	x2		x

	1		1		1		1
no to na przedziale [a;b] masz −		− (−		) =		−
	b		a		a		b

Godzio: No właśnie chcieli, obliczyć całkę górną i dolną i pokazać, że jest sobie równa. A z kolei te całki trzeba było z def. więc końcówka będzie inna, ale wynik wyjdzie ten sam

Basia: no jak z definicji to nie ma zmiłuj, tylko tak na razie