Określ wzajemne położenie prostej L i okręgu o, jesli: (okrąg i koło w układzie Patrycja: Określ wzajemne położenie prostej L i okręgu o, jesli: (okrąg i koło w układzie współrzędnych) a)o: x*2 + y*2 +4x + 6y+8=0 l:y= −5/3x − 5

Huckleberry: Żeby zrobić to zadanie musisz: 1) obliczyć odległość środka okręgu od prostej l korzystając ze wzoru

	|AXS+ByS+C|
d=
	√A2+B2

A i B to są wspołczynniki liczbowe rownania prostej w postaci ogólnej czyli to równanie prostej które masz w zadaniu zamieniasz na rownanie w postaci ogolnej. X_S i Y_S to wspołrzędne środka okręgu i w zadaniu tez musisz zamienic to rownanie okręgu na postac kanoniczną C to to wspołczynnik liczbowy rownania ogolnego twojej prostej. 2) Jak juz zrobisz część punktu 1 tzn okreslisz rownanie ogolne prostej i zamienisz postac ogolna rownania okręgu na postac kanoniczną czyli (x−a)²+(y−b)²=r² to teraz podstawiasz dane do wzoru na odległosc d i loczysz to d. 3) teraz pozostaje pytanie jak okreslic połozenie na podstawie tego co policzyłaś porownujesz to z długoscią promienia okręgu pamietaj ze jak odczytasz go z rownania okręgu postaci kanonicznej to nie jest r² tylko √r jezeli d=r to prosta jest styczną danego okręgu−ma 1 punkt wspolny z okręgiem d<r prosta jest sieczną okregu(ma z nim dwa punkty wspolne) d>r prosta jest zewnętrzna−nie ma punktów wspolnych z okręgiem.

Aga1: lub rozwiązać układ równań x²+y²+4x+6y+8=0

	5
y=−		x−5
	3

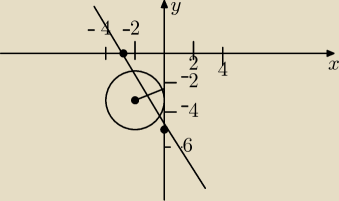
Do pierwszego równania podstawić za y Otrzymasz równanie kwadratowe i jeśli Δ>0 to prosta z okręgiem ma dwa punkty wspólne, jeśli Δ=0 to jest jeden punkt wspólny, natomiast gdy Δ<0 to nie ma punktów wspólnych. Lub po prostu narysować okrąg S=(−2,−3), r=√5 Prosta przechodzi przez punkty (0,−5) i (−3,0)

Aga1: