Jak to rozwiązać?
7733: W ostrosłupie prawidłowym czworokątnym wysokość jest równa 6 i tworzy z krawędzią boczną kąt
45o. Ostrosłup ten przecięto płaszczyzną przechodząca przez przekątną podstawy i nachyloną do
podstawy pod kątem 60o. Oblicz pole otrzymanego przekroju.
Macie jakieś pomysły?
14 lut 17:52
krystek:
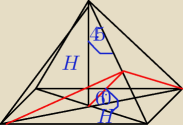
14 lut 17:57
7733:
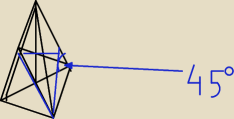
To mój rysunek
14 lut 17:59
7733: przekatna ma 12 tylko jak wysokosc znaleźć
14 lut 18:00
St.: nooo 7733 mógłbyś być malarzem

14 lut 18:01
7733: to jest szkic więc nie wiem co w nim złego
14 lut 18:03
geronimo: Wysokość ma 6√3+6
14 lut 18:08
Basia:
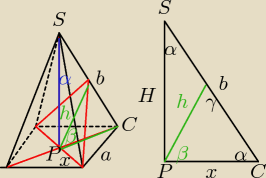
α=45
β=60
x=H = 6 ⇒ d = 12
a przekrój to ten czerwony trójkąt równoramienny
podstawa = d = 12
wysokość h liczysz z drugiego rysunku (tam powinien być trójkąt prostokątny równoramienny)
i tw. sinusów
γ=180−60−45 = 75
14 lut 18:09
geronimo: tam nie będzie konta prostego bo β wynosi 60 więc γ ma 85.
14 lut 18:12
geronimo: źle przeczytałem
14 lut 18:13
7733: Dzięki za pomoc
14 lut 18:14
Basia:
wysokość H jako żywo musi być prostopadła do podstawy i jej przekątnej
a 180 − 60 − 45 jako żywo = 120 − 45 = 120 − 40 − 5 = 80 − 5 = 75
14 lut 18:15
krystek: Połowa przekątnej podstawy =H ponieważ jest tam trójkąt równoramienny prostokątny!
14 lut 18:17

 To mój rysunek
To mój rysunek

 α=45
β=60
x=H = 6 ⇒ d = 12
a przekrój to ten czerwony trójkąt równoramienny
podstawa = d = 12
wysokość h liczysz z drugiego rysunku (tam powinien być trójkąt prostokątny równoramienny)
i tw. sinusów
γ=180−60−45 = 75
α=45
β=60
x=H = 6 ⇒ d = 12
a przekrój to ten czerwony trójkąt równoramienny
podstawa = d = 12
wysokość h liczysz z drugiego rysunku (tam powinien być trójkąt prostokątny równoramienny)
i tw. sinusów
γ=180−60−45 = 75