proszę o pomoc asiulaaa 1818: proszę o rysunek i zapis w graniastosłupie prawidłowym czworokątnym przekątna podstawy ma długość 6 pierwiastków z 2. przekątne dwóch sąsiednich ścian bocznych wychodzące z jednego wierzchołka oraz przekątna podstawy graniastosłupa łączącza końce tych przekątnych tworzą trójkąt równoramienny w którym kąt przy podstawie ma miarę 60 st. oblicz V i Pc tego graniastosłupa

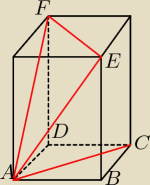
St.: FE − przekątna podstawy = 6√2 AF= AE ∡AFE=∡AEF= 60^o

asiulaaa 1818: a jak resztę obliczyć?

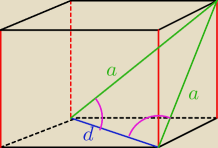
zzzz: d − przekątna podstawy, będą ca podstawą trójkąta równoramiennego a − przekątna ściany bocznej będąca bokiem trójkąta równoramiennego Na różowo zaznaczyłem kąt o którym mowa w zadaniu i mający miarę 60⁰.

asiulaaa 1818: a mogę prosić o całkowite rozwiązanie?

zzzz: Zauważ, że trójkąt o którym mowa w zadaniu jest równoboczny bo ma przy podstawie 2 równe kąty 60^o a trzeci kąt to 180^o − 2*60^o = 60^o.

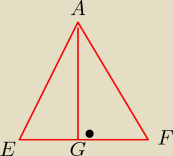
St.: EG = GF = 3√2 Kąty masz podane.Wykorzystaj zależności w trójkącie prostokątnym (sinα=... , cosα=... − obliczysz tym samym bok AF który jest równy boku EA. Następnie korzystasz ze wzorów https://matematykaszkolna.pl/strona/971.html

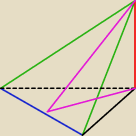
zzzz: Potrzebna jest wysokość i krawędź boczna więc (popatrz na rysunek): Liczę wysokość:

	6√2
H2 + (		)2 = (U{{6√2p[3]}{2})2
	2

Sama wylicz to będzie wysokość... Liczę krawędź podstawy: przekątna kwadratu ma postać a√2, więc: a√2 = 6√2 a = 6 Potrzebna objętość, więc liczysz V i P_c.

zzzz: Poprawię pierwszy wzór na liczenie wysokości:

	6√2		6√2√3
H2 + (		)2 = (		)2, gdzie:
	2		2

6√2
	− połowa przekątnej podstawy
2

U{6√2√3}{2 − wysokość trójkąta równobocznego

asiulaaa 1818: i już tylko podstawić do wzoru?

asiulaaa 1818: (U{{6√2p[3]}{2})2 mógłbyś to poprawić?