Czworokąty Hiromi_Ise: Punkty A, B, C, gdzie A = (2,1), B = (8,5), C = (4,5), są kolejnymi wierzchołkami trapezu ABCD

	1
o podstawach AB i CD. Wiedząc, że |DC| =		|AB|, oblicz współrzędne punktu D oraz cosinus
	2

kąta DAB.

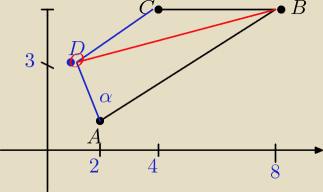
Aga1: IABI=√6²+4²=√52=2√13 ICDI=√13 AB^→=[6,4] DC^→=[3,2] D(x,y) [4−x,5−y]=[3,2] x=1, y=3 Oblicz IBDI W trójkącie ABD skorzystaj z twierdzenia cosinusów.

ejendi: wektor AB={8−2,5−1}={6,4} wektor DC ∥ do AB i 2DC=AB czyli wektor DC={6/2,4/2}={3,2} to współrzędne D=(Cx−DCx,Cy−DCy)=(4−3,5−2)=(1,3) kat DAB=różnicy katów kierunkowych między AD i AB a osią X kąt A=arccos(ADx/|AD|)−arccos(ABx/|AB|) ABx=6 |AB|=√6²+4²=√52 AD={Dx−Ax,Dy−Ay}={1−2,3−1}={−1,2} |AD|=√1+4=√5

	6
cosα1=		=0,832
	√52

	−1
cosα2=		=−0,447
	√5

katα1=33,69 kątα2=116,56 kąt α2−α1=82,87