pochodne, asymptoty, ekstrema, monotonicznosc fynkcji damianno:

	x3
y=
	(x−1)2

1. dziedzina 2. granice na krancach dziedziny 3. y' , przedziały monotonicznosci, ekstrema 4.y" , wklęsłość i wypukłość, punkty przegięcia 5. asymptoty

Aga1: Oblicz coś sam to Ci sprawdzę lub podpowiem.

a: x−1≠0 x≠1 D∊(−∞,1)∪(1,+∞) limx³/(x−1)² = −∞ x→−∞z prawej str limx³/(x−1)²=−∞ x→1 z lewej str limx³/(x−1)² = +∞ x→1 z prawej str limx³/(x−1)²= +∞ x→∞ z lewej str

a: y'=3x²*(x−1)²− x³*(2x−2) x⁴−4x³+3x² −−−−−−−−−−−−−−−−−−−−− = −−−−−−−−−−−−−−− ( (x−1)² )² ( (x−1)²) ²

a: x²(x²−4x+3) = −−−−−−−−−−−−−−− (x−1)⁴

a: funkcja rosnąca ⇔x²(x²−4x+3)>0

a: x=0 lub x²−4x+3=0 Δ=16−12=4 x1= (4−2)/2= 1 x2= (4+2)/2= 3

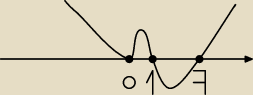
a: f rośnie dla x∊(−∞,1)∪(3,+∞)

a: f maleje dla x∊(1,3)

a: ekstrema są w punkcie 3 ( 1 nie należy do dziedziny) funkcja zmienia znak w punkcie 3 z − na + dlatego 3−maksimum lokalne f(3)=27/4