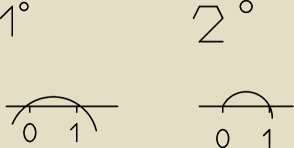Gdzie robię błąd? nieuk: rozwiąż nierówność. ^|1−x|_x<0 Dziedzina: R\{0} korzystam z tego, że |x|<a <=> −a<x<a mam 2 przypadki 1^o x∊(−∞;0) ⋀ 2^o x∊(0;∞) 0<^1−x_x ^1−x_x<0 −(x−1)x>0 −(x−1)x<0 odczytuje z wykresów przedziały x∊(0;1) x∊(−∞;0)u(1;∞) sprawdzam z zał. 1^o sprawdzam z zał. 2^o i mam zbiór pusty x∊(1;∞) biorę iloczyn (cz. wspólną) obu przypadków i mam zbiór pusty... a w odp jest x∊(−∞;0)

Aga1: Źle rozpatrujesz przypadki I1−xI=1−x, gdy 1−x≥o, czyli x≤1i x≠0 I1−xI=−(1−x)=x−1, gdy 1−x<0, tzn gdy x>1.

pigor: ... a tak w ogóle, to ja proponuje np. tak :

|1−x|
	< 0 ⇔ x< 0 i 1−x ≠0 ⇔ x<0 i x ≠1 ⇔ x< 0, czyli x∊(−∞;0) .
x

nieuk: ok mam te 2 przypadki: 1^o x∊(−∞;1) i 2^o x∊(1;∞) ^−(1−x)_x<0 ^(1−x)_x<0 (x−1)x<0 −(x−1)x<0 x∊(0;1) x∊(−∞;0)u(1;∞) x należy do zał do zał należy tylko (1;∞) i mam wziąć iloczyn, co daje mi zbiór pusty... co jest sprzeczne z odp.

pigor: ... no to ja jeszcze raz , daj sobie spokój ze schematami; licznik masz dodatni dla każdego x≠1(x=1 nie spełnia danej nierówności) , więc go olej, wtedy cały ułamek zależy od mianownika , który powinien być ujemny, aby cały ułamek był ujemny , czyli x<0 i ... tyle

nieuk: yhym... czyli każdy przykład wymaga indywidualnego podejścia − nie robić schematami... dzięki

pigor: TAK no właśnie , . ... o to chodzi i bardzo się cieszę , że wreszcie to do ciebie dotarło , bo żal patrzyć jak się męczycie na tym forum, zamiast nauczyć myśleć