obliczanie pola graniastosłupa KASIA: 1.oblicz długość krawędzi bocznej i długości krawędzi podstawy graniastosłupa prawidłowego sześciokątnego którego najdłuższa przekątna wynosi 3√5 a pole powierzchni bocznej 54. 2. podstawą graniastosłupa prostego jest równoległobok o bokach 6 i 4 oraz o kącie 60 stopni. wiedząc że krótsza przekątna ma długość 4√3 oblicz pole powierzchni bocznej tego graniastosłupa. W MIARĘ MOŻLIWOŚCI PROSZĘ O RYSUNKI

Anna: pomagam

Anna: Kasiu, sprawdź dane do zad. 1. (pojawia się sprzeczność, brak rozwiązania)

Anna: Przepraszam, to ja spisałam złą wartość przekątnej,poczekaj moment. Zaraz piszę.

Anna:

	9
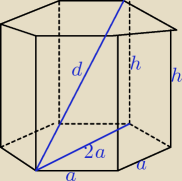
Pb=6ah ⇒6ah = 54 /:6 ⇒ah = 9 ⇒ h =
	a

Z rys. , z trójkąta mamy: h²+(2a)² = d² h²+4a²=(3√5)²

	9
(		)2 +4a2 = 45
	a

81
	+ 4a2= 45 /*a2
a2

81 +4a² = 45a² 4a² − 45a² + 81= 0 Podst. a² = t ⇒ 4t²−45t + 81 = 0

	9
Δ=729, √Δ = 27, t1=9, t2=
	4

t=9 ⇒ a² =9 ⇒ a=3 , h = 3 lub

	9		9
t=		⇒ a2=		⇒ a= 1.5, h = 6
	4		4

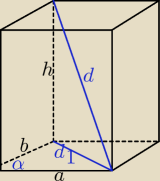
Anna: zad. 2. a=6, b=4, α=60⁰, d=4√3, P_b=? P_b= 2ah + 2bh Ze wzoru cosinusów: d₁² = a²+b²−2abcosα d₁² = 6²+4²−2*6*4*cos60⁰ d₁² =28 ⇒ d₁ = √28 = 2√7 h²+d₁² = d² h²+28= (4√3)² h²=48−28 ⇒ h=2√5 P_b=2*6*2√5 + 2*4*2√5 = 24√5 + 16√5 = 40√5