Srereometria Mati: Wysokość prostopadłościanu jest trzy razy dłuższa niż krawędź kwadratu w jego podstawie.Przekątna ściany bocznej jest nachylona do płaszczyzny podstawy pod kątem α takim ,że:

	√10
Prawidłowa odpowiedz cos α =
	10

Bardzo proszę o wyjaśnienie tego zadania.

Mati: kiedyś pomagaliście teraz ostatnio nikt nie ma czasu

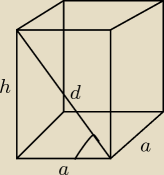konrad: cos α=a/d h=3a d=√(3a)²+a² d=√9a²+a² d=√10a² d=a√10

	a
cos α=
	a√10

	√10
cos α=
	10

Mati: dzięki wielkie Konrad

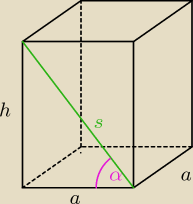dero2005: krawędź podstawy wynosi a, wysokość jest trzy razy większa, więc h = 3a przekątna ściany bocznej s wynosi (liczymy z pitagorasa) s = √a² + h² = √a² + (3a)² = √a² + 9a² = √10a² = a√10 cosinus α wynosi

	a		a		1*√10		√10
cos α =		=		=		=
	s		a√10		√10*√10		10