Rozwiaz nierownosc
Handball93: | (x + 3)(x2 −5x +6) | |
|
|
| (x2 −9)(x−3) | |
czemu 3 i −3 sa miejscami zerowymi skoro nie naleza do dziedziny

12 lut 17:08
Zak z rasy joonów : Ponieważ są podwójne. Przy rozwiązywaniu nierówności wykres odbija się od podwójnych miejsc
zerowych.
12 lut 17:09
Handball93: a jak sa potrojne to co wtedy?
12 lut 17:10
Kejt: na pewno dobrze to przepisałeś..? mi wyszło, że miejscem zerowym jest tylko 2.
12 lut 17:10
Kejt: dobra..nic nie mówiłam.
12 lut 17:11
Handball93: poza tym −3 jest pojedynczy
12 lut 17:11
Handball93: tam ma byc to rownanie wieksze lub rowne zero Kejt

12 lut 17:12
Zak z rasy joonów : nie. Jest podwójny.
12 lut 17:12
Handball93: dlaczego?
12 lut 17:13
Kejt: | | (x+3)(x−2)(x−3) | |
= |
| |
| | (x+3)(x−3)(x−3) | |
12 lut 17:13
Handball93: (x−3) sie skracaja

wiec jest pojedynczy
12 lut 17:14
Zak z rasy joonów : te moje przyzwyczajenia

Jak skrócisz zostaje ci :
| x−2 | |
| ≥ 0 ⇔ x ∊ (−∞;2> suma (3;+∞) |
| x−3 | |
12 lut 17:21
Handball93: wlasnie tak zrobilem, ale jest zle.
(−∞,−3)u(−3,2>u(3,+∞)
czemu zmieniasz nick? nie wiem jak mam sie zwracac..
12 lut 17:28
Zak z rasy joonów : wstyd

Dziedziny nie ustaliłem...
D : x ∊ R\{−3;3}
wiec −3 trzeba też wyrzucić z rozwiązania.
12 lut 17:30
Handball93: no wlasnie to czemu −3 jest msc zerowym

12 lut 17:31
Zak z rasy joonów : nie jest. Nie ma go w dziedzinie

12 lut 17:31
Handball93: rozwiazanie mam dobre wiec nie potrafisz zrobic zadania

12 lut 17:31
Zak z rasy joonów : bo prostu robię za szybko i pomijam podstawowe rzeczy

Za proste

12 lut 17:35
Kejt: czyli miałam rację..pierwiastkiem jest tylko 2

12 lut 17:35
Zak z rasy joonów : Niom

12 lut 17:35
Handball93: nie, moje rozwiazanie jest dobre

oboje macie zle, albo masz zle

12 lut 17:36
Zak z rasy joonów : więc pokaż mi mój błąd.
12 lut 17:37
12 lut 17:38
Aga1:
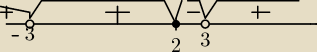
(x−2)(x+3)≥0
x∊(−
∞,−3)∪(−3,2>∪(3,
∞)
12 lut 17:44
Handball93: mozesz mi to rozpisac

12 lut 19:00
Aga1: Właściwie to prawie wszystko zostało napisane. zaczynasz od dziedziny
(x
2−9)(x−3)≠0
x≠−3 i x≠3
Rozkładasz licznik i mianownik na czynniki (i to było zrobione), skracasz i zostaje Ci
(x−3)(x−2)≥0
Teraz rysujesz parabolę ramionami do góry. odczytujesz rozwiązanie uwzględniając dziedzinę.
12 lut 19:07
Handball93: ale czemu −3 jest msc zerowym

12 lut 19:27
Aga1: x2−9≠0 Korzystasz ze wzoru skróconego mnożenia ( w najgorszym przypadku z Δ)
(x−3)(x+3)≠0
I dalej
x−3≠0 i x+3≠0
x≠3 i x≠−3.
12 lut 19:30
Handball93: no ale czemu −3 nie jest w dziedzinie a jest msc zerowym

12 lut 19:33
Handball93: hmm ?
12 lut 19:49
Kejt: gdzie Ty masz napisane, że jest miejscem zerowym?

12 lut 19:50
Handball93: x∊(−∞,−3)∪(−3,2>∪(3,∞)
12 lut 21:14
luk: Witam mam takie zadanie oblicz granice:
12+22+...+n2n3 =
w rozwiazaniu jest takie przeksztalcenie 12+22+...+n2=n(n+1)(2n+1)6
moze mi ktos wytlumaczyć skąd to przekształcenie wynika?
12 lut 21:22
Aga1: Jest taki wzór, można go udowodnić indukcyjnie.
13 lut 09:37
Kejt: zauważ, że −3 nie należy do tego zbioru..
13 lut 12:51


 wiec jest pojedynczy
wiec jest pojedynczy
 Jak skrócisz zostaje ci :
Jak skrócisz zostaje ci :
 Dziedziny nie ustaliłem...
D : x ∊ R\{−3;3}
wiec −3 trzeba też wyrzucić z rozwiązania.
Dziedziny nie ustaliłem...
D : x ∊ R\{−3;3}
wiec −3 trzeba też wyrzucić z rozwiązania.



 Za proste
Za proste


 oboje macie zle, albo masz zle
oboje macie zle, albo masz zle 
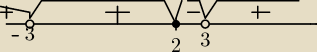 (x−2)(x+3)≥0
x∊(−∞,−3)∪(−3,2>∪(3,∞)
(x−2)(x+3)≥0
x∊(−∞,−3)∪(−3,2>∪(3,∞)



