Stożek 00x: Przekrój osiowy stożka jest trójkątem równobocznym o wysokości 6. W stożek wpisujemy różne graniastosłupy prawidłowe trójkątne tak, że jedna podstawa graniastosłupa jest zawarta w podstawie stożka, a wierzchołki drugiej leżą na powierzchni bocznej stożka. Wyznacz wymiry takiego graniastosłupa , którego pole powierzchni bocznej będzie największe.

Mila: obliczamy bok Δ (a√3)/2 =6 a=4√3 R =2√3 − promień w postawie stożka Graniastosłup jest prawidłowy− w podstawie ma Δ równoboczny Liczę dalej, możesz podać odpowiedź? Spróbuję narysować . Wejdę na komputer po 20 .

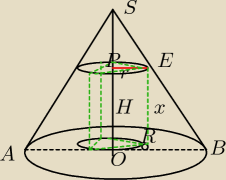
Mila: H=6 R=2√3 ΔSPE jest podobny do ΔSOB

H−x		H		6−x		6
	=		⇔		=
r		R		r		2√3

oblicz r a następnie wysokość górnego trójkąta równobocznego i jego bok w zależności od x. Pb (x) =3*b*x będzie funkcją kwadratową i obliczysz dla jakiego x ma wartość największą.