Trygonometria Godzio: Kejt zerknij tu

Zak z rasy joonów : no jestem

Godzio: https://matematykaszkolna.pl/forum/55180.html −− tu jest parę zadań dla Kejt, nie wszystkie rozwiązania w tym temacie są prawidłowe, więc nie musisz się nimi sugerować

Zak z rasy joonów : Dziękuję Godziu

Godzio: To Ty w końcu ?

Aga1: Jednak nie nadaję się na detektywa.

Godzio:

Zak z rasy joonów : Tak to ja

Kejt: mm..mieszanka trygonometryczna..moja ulubiona..skąd wiedziałeś?

Kejt: 1 i 4 praktycznie nie mogę ruszyć.. w drugim utknęłam przy:

7
	(sinx+cosx)
8

a trzecie zrobione bez problemu.. robię dalej..

Godzio: Jeśli chcesz sprawdzenia czy coś, to pisz zadanie tutaj i do niego rozwiązanie, jeśli wskazówki to też zadanie i wtedy mogę coś pomóc, bo nie chce mi się łazić po linkach

Kejt: ok.

	1
Obliczyć sin3x+cos3x mając dane sin2x=
	4

doszłam do:

7
	(sinx+cosx)
8

i nie mam pomysłu co dalej..

Zak z rasy joonów : (sinx+cosx)² = 1 + sin2x

Godzio: sin²x + cos²x = 1 Zatem sinx + cosx = ?

Kejt: √1+sin2x..?

Godzio: Mały błąd (niedokładność )

Kejt: hmm.. sin²x+cos²x=1 sin²x+2sinxcosx+cos²x=1+2sincosx (sinx+cosx)²=1+sin2x /√ |sinx+cosx|=√1+sin2x? nie rozumiem o co zbytnio chodzi..

Godzio: No teraz ok Czyli sinx + cosx = ?

Kejt: −√1+sin2x v √1+sin2x?

Godzio: Jawohl !

Kejt: ach..dopiero teraz zajarzyłam do czego ma mi się to przydać wyszło:

7√5		7√5
	v −
16		16

Godzio:

Kejt: Dla jakich wartości sinx liczby sinx, cosx, sin2x ( w podanym porządku ) są kolejnymi wyrazami ciągu geometrycznego? Wyznaczyć czwarty wyraz tego ciągu dla każdego z rozwiązań. robię tak: z własności ciągu geo: cos²x=sinx*sin2x robiłam na dwa sposoby: za pierwszym wyszło mi tak:

	1
1) −cos2x−		cosx+1=0
	2

t=cosx t∊<−1;1>

	1
−t2−		t+1=0
	2

	1		17
Δ=		+4*1=
	4		4

delta wyszła nieciekawa więc dalej zostawiłam.. 2) cosx(−2sin²x+cosx)=0 cosx=0 v −2sin²x+cosx=0 cos2x+cosx=1 i dalej też nie wiem

Godzio: cos²x = sinx * sin2x cos²x = 2sin²xcosx cos²x = 2(1 − cos²x)cosx cos²x = − 2cos³x + 2cosx 2cos³x + cos²x − 2cosx = 0 Działaj dalej . Mam jedną prośbę, jeśli robisz zadanie, staraj się je robić dokładnie, nie chce być upierdliwy, ale czasem nudne jest pisanie oczywistości

Godzio: Cofam swój post Zadanie jest ok, tylko hmmm, zadanie nieciekawe

Godzio: Dobra, przeczytaj polecenie

Kejt: no ja wiem, że trzeba to doprowadzić do sinusa..ale za cholerę nie wiem jak..

Kejt: dobra..mniejsza z tym..spróbuję jeszcze rano..teraz idę spać..dobranoc.

Godzio: Wiesz co, idź tą drogą co robiłaś, wyniki w odpowiedzi są paskudne, więc droga jest ok, po wyliczeniu cosx wyznaczysz przez jedynkę trygonometryczną sinx

Kejt: pierwszą czy drugą drogą?

Godzio: Obojętnie, tyle, że z drugiej cosx = √1 − sin²x

Kejt: wyszło:

	√43+4√17		√43+4√17
sinx=		v sinx=−
	8		8

	455√17−234
a4=
	13

przy liczeniu drugiego a₄ po podniesieniu do kwadratu sin2x zaczęło wychodzić to samo, więc zostawiłam..

Kejt: wyszło:

	√43+4√17		√43+4√17
sinx=		v sinx=−
	8		8

	455√17−234
a4=
	13

przy liczeniu drugiego a₄ po podniesieniu do kwadratu sin2x zaczęło wychodzić to samo, więc zostawiłam..

Kejt:

	π		π
Rozwiązać nierówność sin2x<sinx w przedziale <−		;		>
	2		2

wychodzi mi: sinx(2cosx−1)<0 sinx=0 v 2cosx−1=0 2cosx=1

	1
cosx=
	2

	π		2π
x=		+2kπ v x=		+2kπ
	3		3

jak ja mam to narysować? żeby uwzględnić przedział..

Godzio: 2cos³x + cos²x − 2cosx = 0 cosx = 0 lub 2cos²x + cosx − 2 = 0 ⇒ Δ = 17

	− 1 + √17		− 1 − √17
cosx =		lub cosx =		−− to drugie oczywiście odpada
	4		4

	1 − 2√17 + 17		9 − √17		8 − 9 + √17
sin2x = 1 −		= 1 −		=		=
	16		8		8

	√17 − 1
=
	8

	√√17 − 1
Zatem: sinx = ±
	2√2

Dla cosx = 0 mamy: sin²x =1 ⇒ sinx = ±1 Czwarty wyraz: Dla sinx = ± 1 a₄ = 0

	√√17 − 1
Dla sinx = ±		mamy:
	2√2

	− 1 + √17		√√17 − 1		√√17 − 1
2 *		* ±		* 2 * (±		) =
	4		2√2		2√2

	√17 − 1		17 − 2√17 + 1		9 − √17
(− 1 + √17)*				=
	8		8		4

Godzio: Kejt jak się rozwiązuje nierówności ? sin2x < sinx Rozwiązujesz równanie: sin2x = sinx 2x = x + 2kπ lub 2x = π − x + 2kπ Mając punkty przecięcia rysujesz sobie oba wykresy i odczytujesz rozwiązanie, tyle.

Kejt: nie wiedziałam jak to narysować..ale..mniejsza z tym..

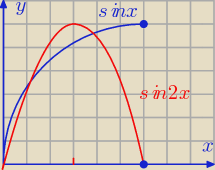
Godzio: Jak to nie wiedziałaś jak narysować ?

Kejt: mam dziwne wrażenie, że z każdym zdaniem coraz bardziej się pogrążam..

Godzio:

	π		π
No dobra, rozwiązanie chciałbym Pamiętaj, przedział jest [−		,		]
	2		2

Kejt:

	π
x∊<−		;0)?
	2

jeśli nie..to ja się poddaję..

Godzio:

	π
Przecież na rysunku w przedziale [0,		] widać gołym okiem rozwiązanie
	2

Godzio:

	π		π		π
x ∊ (−		,0) U (		,		]
	3		3		2

Godzio: Ten mój rysunek tutaj, to taki nieciekawy, bo nie oddaje w pełni sin(2x)

Kejt: już wiem..po prostu bardzo inteligentnie(patrząc na wykres) stwierdziłam, że −π/2>−1..nie komentujmy tego proszę.. i zły wykres miałam −.−

pigor: ... Kejt, nie załamuj się, bo np. ja nie chciałbym korzystać z tak "kłamliwego" wykresu i proponuję metodę analityczną taką : sin2x< sinx ⇔ 2sinxcosx−sinx< 0 ⇔ sinx(2cosx−1)< 0 ⇔ (sinx< 0 i 2cosx−1 >0) lub (sinx >0 i 2cosx−1< 0) ⇔ (sinx< 0 i cosx >¹₂) lub (sinx >0 i cosx< ¹₂) i teraz już prosto podać sumę rozwiązań w danym przedziale [−^π₂; ^π₂] . ... pozdrawiam

Kejt: Pigor, dziękuję..już sobie to wyrysowałam w programie i wszystko mi się zgadza..po prostu zamiast sinx miałam wykres cosx..

Godzio: Lepiej starannie sobie wykres narysować (bez programów), metodą analityczną zajmuje to znacznie więcej czasu, ale lepiej go nie tracić (jak rysowałem wykres to nie zwróciłem uwagi na szczegóły i wyszedł jak wyszedł ... )

Kejt: Wykazać, że dla każdego kąta α prawdziwa jest nierówność: √3sinα + √6cosα ≤ 3 mogę jakąś wskazówkę? bo mi nie wychodzi..

Godzio: Może tak jak AS w rozwiązaniu zaproponował i zrobił, ale na razie tam nie zaglądaj Podziel na √3 i wprowadź oznaczenie: tgβ = √2

Kejt: wyszło mi:

	π
sin(α+β)≤tg		*cosβ
	3

Godzio: cosβ = ?

Kejt:

sinβ
	?
√2

pigor: a co powiesz, jeśli wiesz przecież, że cosβ ≤ 1 , to . ...

Godzio:

sinβ
	= √2
cosβ

sinβ = √2cosβ sin²β = 2cos²β

	1
1 = 3cos2β ⇒ cosβ = ±
	√3

	1
Dla cosβ =
	√3

	1
sin(α + β) ≤ √3 *		= 1
	√3

	1		√2
Dla cosβ = −		(sinβ = −		)
	√3		√3

	1		√2
sinα * (−		) + cosα * (−		) ≤ √3 / * (−√3)
	√3		√3

sinα + √2cosα ≥ − 3 A to już oczywiste ponieważ: sinα ≥ − 1 √2cosα ≥ − √2 sinα + √2cosα ≥ − 1 − √2 ≥ − 3 (tą ostatnią nierówność też można pokazać )

Kejt: ach...dlatego nie wychodziło..po tym jak mnie okrzyczeliście za podnoszenie do kwadratu nawet mi to przez myśl nie przechodzi..