zbadać monotoniczność i wyznaczyć ekstrema lokalne
łoki: pomóżcie
11 lut 19:43
Grześ: Pokaż jak liczysz pochodną
11 lut 19:48
11 lut 19:53
Grześ: Dobrze, teraz określ dziedzinę funkcji, oraz dziedzinę pochodnej.
Przyrównaj licznik do zera
i rozwiąż równanie
11 lut 19:55
11 lut 19:55
łoki: x≠0 ?
11 lut 19:56
łoki: −lnx=0
11 lut 19:57
łoki: dobrze?
11 lut 19:58
łoki: pomoże ktoś dalej
11 lut 20:16
Grześ1992:
x>0 jeszcze....
e
0=x ,czyli x=1
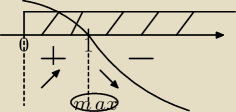
oś pochodnej narysuj zaznacz dziedzinę, punkt przecięcia z osią OX i gdy przyrównywałeś do 0
zaraz na początku musisz już wtedy określić znak przy największej potędze i jeżeli już
zauważysz że jest ujemna wtedy rysujesz jak idzie ta pochodna a więc od prawej strony wykres
idzie od dołu do 1 i przebija się przez oś OX ponieważ 1 jest nieparzysty... gdy wykres jest
nad osią piszesz + gdy pod osią − oczywiście tylko tam gdzie dziedzina . Tam gdzie +
funkcja(nie pochodna) rośnie a gdzie − maleje.
zauważasz że w punkcie 1 jest maksimum lokalne
11 lut 20:26
Grześ1992: poprawcie mnie jeżeli coś źle powiedziałem
11 lut 20:27
łoki: rośnie (0;
√e)
maleje (
√e;+
∞)
max lok x=
√e
tak mam w odpowiedziach
11 lut 20:43