..
110x0010x0: Udowodnij, że dla każdego x∊(0;+∞) x>sinx
11 lut 13:27
110x0010x0: up
11 lut 19:37
110x0010x0: up
11 lut 23:32
Godzio:
Spróbuję udowodnić
11 lut 23:38
Godzio:
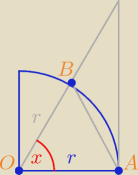
Prosty dowód geometryczny:
P
OAB < P
wycinka koła
| 1 | | x | | 2 | |
| * r2 * sin(x) < |
| * πr2 / * |
| |
| 2 | | 2π | | r2 | |
sin(x) < x
11 lut 23:43
Godzio:
| | π | |
Dodam, że zadanie sprowadza się do pokazania, że nierówność zachodzi dla x ∊ (0, |
| ] bo to |
| | 2 | |
| | π | |
w |
| sinus osiąga maxa, jak wcześniej nie przewyższy x co do wartości to już nigdy tego |
| | 2 | |
nie zrobi
11 lut 23:51
Godzio:
| | π | |
ICSP i ZKS zachęcam was do pokazania, że w dla x ∊ (0, |
| ) zachodzi nierówność: |
| | 2 | |
x < tgx
ZKS, a później udowodnimy coś ciekawszego, czego używałeś, a nie koniecznie miałeś tego
dowód. A
ICSP za pewne go pozna w niedługiej przyszłości
11 lut 23:54
ZKS:
Zawsze spróbować można.
12 lut 00:16
Godzio:
I jak idzie
?
12 lut 00:42
ZKS:
Jak po grudzie.
I teraz się zastanawiam jak by tego cosinusa inaczej zapisać żeby zamienić na sinusa.
12 lut 00:47
Godzio:
A po co zrobiłem taki ładny rysunek ! Dowód geometryczny, rachu ciachu i koniec
12 lut 00:49
ZKS:
Jak sam napisałeś dowód geometryczny a ja tak bardzo je lubię ale może coś z wykombinuje.
12 lut 00:53
Godzio:
Rozumowanie takie samo jak sinx < x
12 lut 00:54
ZKS:
| x | | 1 | |
| * πr2 < |
| * r2 * tgx |
| 2π | | 2 | |
?
12 lut 00:56
Godzio: 
12 lut 00:57
Godzio:
No dobra, w takim razie skoro tyle wiem:
sinx < x < tgx
| | sinx | |
To pokażmy, że limx→0+ |
| = 1 |
| | x | |
Miałeś ten dowód ? Jeśli nie to próbuj, ale zanim co, chciałbym, żebyś pomyślał dlaczego
wystarczy x → 0
+
Jeśli masz ochotę oczywiście, staram się urozmaicać trochę
12 lut 00:59
ZKS:
Ja nie mam żadnych dowodów u siebie po prostu musimy wiedzieć i później wykorzystywać to.
Na
razie jeszcze mam ochotę ale zobaczymy później hehe.
12 lut 01:05
Godzio:
No to jak będziesz chciał, to czasem możemy sobie wyprowadzić takie standardowe wzory ze
studiów
Przyda mi się powtórka
12 lut 01:07
ZKS:
I co z tym zrobić?
12 lut 01:07
ZKS:
Twoja ulubiona analizka matematyczna co?
Czy jakiś inny dział?
12 lut 01:09
Godzio:
Ano analiza
Rób na obu stronach przekształcenia. tzn
sinx < x < tgx
itd...
12 lut 01:11
ZKS:
Okej.
12 lut 01:15
Godzio:
Coś długo to ciągniesz, to może dam jeszcze jedną wskazówkę
| | sinx | |
1 > |
| > cosx = 1 − 2sin2x2 < ... |
| | x | |
12 lut 01:33
Godzio:
Yyy, zanim < ..., trzeba zrobić małe przekształcenie, żeby nam się znaki zgadzały
< ... < ...
12 lut 01:34
ZKS:
| | sinx | |
cosx − 1 < |
| − 1 < 0 |
| | x | |
| | x | | sinx | |
−2sin2 |
| < |
| − 1 < 0 |
| | 2 | | x | |
| | sinx | | x | |
0 < 1 − |
| < 2sin2 |
| |
| | x | | 2 | |
| | x | | x | | π | |
sin2 |
| < sin |
| ponieważ sinx dla x ∊ (0 ; |
| ) jest ułamkiem mniejszym od 1 to |
| | 2 | | 2 | | 2 | |
liczby podniesione do kwadratu będą mniejsze więc
| | sinx | | x | |
0 < 1 − |
| < 2sin |
| |
| | x | | 2 | |
| | x | |
a skoro wiemy że sinx < x to można przyjąć że sin |
| < x |
| | 2 | |
Dalej nic nie wymyślę.
12 lut 01:39
Godzio:
Już Cię nie męczę
| | sinx | |
1 > |
| > 1 − 2sin2x2 odejmijmy 1 i przemnóżmy przez (−1) |
| | x | |
| | sinx | | x2 | |
0 < 1 − |
| < 2sin2x2 < 2 * |
| = x2 → 0 przy x → 0+ |
| | x | | 2 | |
Z twierdzenia o trzech funkcjach mamy:
| | sinx | | sinx | |
1 − |
| → 0 zatem |
| → 1 |
| | x | | x | |
Dobra, ale dlaczego mogliśmy badać tylko x → 0
+ ?
12 lut 01:42
ZKS:
Pomyślę ale raczej nie oczekuj że podam odpowiedź tylko się mogę zastanowić nad tym.
Daj mi
5 − 10 min.
12 lut 01:45
Godzio:
Ale byłeś już o ciut od rozwiązania
12 lut 01:48
ZKS:
| | sinx | | sin(−x) | |
Hmm no to tak myślę że dlatego że |
| = |
| |
| | x | | −x | |
| | sin(−x) | | −sinx | | sinx | |
bo |
| = |
| = |
| ? |
| | −x | | −x | | x | |
12 lut 01:49
Godzio:
| | sinx | |
Tak, po prostu |
| to funkcja parzysta |
| | x | |
12 lut 01:49
Godzio:
Jeśli chcesz jeszcze coś udowodnić, to daj twierdzenie czy coś to pobawimy się
Ja chyba do 4
nie będę spał jak zwykle więc będzie mi się nudzić
12 lut 01:50
ZKS:
Ach czuję się teraz mądrzejszy o 100% tego co umiałem heh.
12 lut 01:51
ZKS:
Kurde szkoda że jutro w nocy nie będziesz wolny (bo idziesz już na uczelnie) to wtedy byśmy
sobie porobili coś bo ja muszę rano wstać niestety. Ale mam nadzieje że kiedyś jeszcze w BF
zagramy.
12 lut 01:53
Godzio:
Kiedyś ... zawsze możemy
A w poniedziałek mam na 13
12 lut 01:54
ZKS:
Oo no to chyba że będziesz mógł to jutro byśmy jakieś zadanka przerobili?
Skoro do 4 nie
będziesz dzisiaj spał to zagraj sobie.
Brat wraca w środę dopiero więc wtedy będę mógł
pograć ale Ty wtedy będziesz miał naukę na pewno.
12 lut 01:58
Godzio:
A tam, pierwszy tygodnie
A już się dzisiaj nagrałem, także raczej dzisiaj już nie
12 lut 01:59
ZKS:
A wtedy co Cie wyrzuciło z serwera to grałem do 6.
Dobrze że jeszcze mam tydzień wolnego ale
mam nadzieje że tydzień który rozpocznie 2 semestr będzie lajtowy.
12 lut 02:05
Godzio: Też mam taką nadzieję
12 lut 02:07
ZKS:
To może jeżeli nie będziesz spał to może dam Ci nierówność jakąś i Cię opuszczę?
12 lut 02:10
Godzio:
No to możesz dać
12 lut 02:12
ZKS:
Już Ci ją podaję.
12 lut 02:16
ZKS:
Dla a > 0 ; b > 0 ; x > 0 ; y > 1 ; b > x
√(ya)2 + (yb + x)2 +
√a2 + (b − x)2 >
√(ya)2 + (yb)2 +
√a2 + b2 oraz
√a2 + (b + x)2 +
√(ya)2 + (yb − x)2 >
√(ya)2 + (yb)2 +
√a2 + b2.
12 lut 02:18
Godzio: Ooooo tak
Myślę, że do końca życia to rozwiążę
12 lut 02:19
ZKS:
Mam nadzieję że w końcu coś Ci dałem nie na 5 min roboty dla Ciebie.
12 lut 02:21
ZKS:
No dobra bo jutro to chyba nie wstanę o tej o której muszę.
Dobranoc i życzę Ci powodzenia z
zadaniem.
12 lut 02:24
Godzio:
Dzięki
12 lut 02:27
Godzio: I dobranoc !
12 lut 02:27
Godzio:
1.
Jak podniosę do kwadratu to otrzymam coś w tym stylu:
bx(y − 1) +
√m + t >
√t
Gdzie m > 0, a z założeń bx(y − 1) > 0
Samo wymnożenie pierwiastka mi zajęło 2 linijki na długość A4, także nawet tutaj tego nie
przepisuje
12 lut 02:49
110x0010x0: Fajny wątek, często nie wiadomo skąd różne rzeczy się biorą a tu proszę dowiedziałem się o paru
wyprowadzeniach
12 lut 12:04