Planimetria
Dlaczemu nie?: Potrzebuję wsparcia i rysunku


W trójkącie ostrokątnym ABC z wierzchołków A i C opuszczono wysokości AD i CE na boki BC i AB.
Wykaż, że trójkąty ABC i BDE są podobne.
W końcowej fazie zostaje mi trójkąt i nie potrafię jego kątów uzależnić od reszty kątów prze
zemnie wyliczonych... Jak wprowadzę dwa dodatkowe oznaczenia to wychodzi błędne kolo...
10 lut 23:29
Dlaczemu nie?: Pomoże ktoś?

10 lut 23:51
Dlaczemu nie?: Arturze ratuj

11 lut 00:37
Artur z miasta Neptuna:
czytam
11 lut 00:59
Artur z miasta Neptuna:
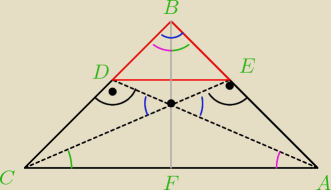
Tak naprawdę to zadanie polega na udowodnieniu, że tak skonstruowany odcinek DE jest || do AC.
11 lut 02:23
Bizon:
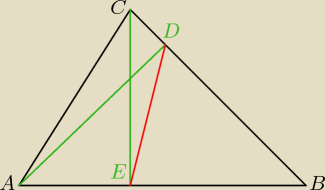
... a oczywiśce nie jest ...
11 lut 08:27
Zuzik P: Bizon pomożesz za pół godziny? 30zł przelewem/>
11 lut 09:02
Dlaczemu nie?: to co z tym robić?
11 lut 09:15
Bizon:
... a dobrze przepisałeś zadanie

?
11 lut 09:36
Dlaczemu nie?: tak

11 lut 09:45
Bizon: jaki to trójkąt ... równoramienny ... równoboczny

? ...
11 lut 09:48
Dlaczemu nie?: Ostrokątny

nic więcej nie ma w zadaniu

11 lut 09:50
Dlaczemu nie?: dla trójkątów równoramiennego i równobocznego zadanie wyglądałoby tak jak pisał Artur. Niestety
trzeba udowodnić dla trójkąta dowolnego, ale jak to zrobić...?
11 lut 09:57
Bizon: nie jest ... więc nie udowodnisz ...
11 lut 10:03
Artur z miasta Neptuna:
Mam ... udowodniłem ... ale babrać się trzeba niemiłosiernie.
Postaram się to ładnie pokazać.
Moje poprzednie założenie było błędne, ale dowód jest

11 lut 13:04
Artur z miasta Neptuna:
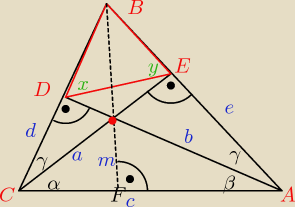
Rysunek ... baaaardzo duży powinien być

Z ΔACD mam, że α+β+γ = 90
o
Wtedy patrząc na ΔACE wiem, że nad β także jest kąt γ
Punkt przecięcia się prosty nazywam 'S'.
ΔCSD podobny do Δ ASE (te same kąty).
na
niebiesko podaję długości odcinków.
na
zielono szukane kąty
ΔACE podobny do ΔSCF.
ΔDAC podobny do ΔFAS.
....
11 lut 13:25
Artur z miasta Neptuna:
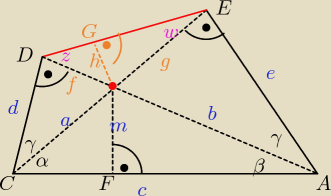
patrzę na ten czworokąt.
fioletowe oznaczenia są to miary kątów.
Z podobieństw, które zapisałem wcześniej mam:
| a | | c | | b | | c | | a | | d | |
| = |
| ⋀ |
| = |
| => ae = bd => |
| = |
| (1) |
| m | | e | | m | | d | | b | | e | |
Z podobieństwa ΔCSD i Δ ASE mam:
| d | | e | | f | | d | |
| = |
| => |
| = |
| (2) |
| f | | g | | g | | e | |
| | h | | h | | f | | sin w | |
sin z = |
| ⋀ sin w = |
| => f*sin z = g*sin w => |
| = |
| (3) |
| | f | | g | | g | | sin z | |
patrząc na (1), (2) i (3) wnioskuję, że:
a wiadomo, że:
| a | | am | | sin β | |
| = |
| = |
| |
| b | | bm | | sin α | |
więc:
| sin w | | sin β | |
| = |
| |
| sin z | | sin α | |
przypadek 1.
z = α ... wtedy w = β
z poprzedniego rysunku wiem, że w+x = 90
o => x = 90
o − α = β+γ ⋀ analoginie y = α+γ
czyli −−− c.n.d.
przypadek 2
z ≠ α ... wtedy w ≠ β
Wiem, że: ∡CSA = ∡ESD ⋀ ∡CSA = 180−α−β
niech z = α−ε ... wtedy w = 180 − (180 − α − β) − z = β + ε ....
ε≠0
więc mam:
| sin (β + ε) | | sin β | |
| = |
| |
| sin (α − ε) | | sin α | |
| sin βcos ε + cos βsin ε | | sin β | |
| = |
| |
| sin αcosε − cos αsinε | | sin α | |
sin αsin βcos ε − cos αsin βsin ε = sin αsin βcos ε + sin αcos βsin ε
− cos αsin βsin ε = sin αcos βsin ε /: sin ε
− cos αsin β = sin αcos β
cos αsin β + sin αcos β = 0
sin (α+β) =0
czyli: α+β = 0 + 2kπ (k=0 lub k=1)
więc α = −β <− sprzeczne lub α = 180 − β
na samym początku napisałem:
α+β+γ = 90 ... podstawiam i wychodzi:
180 − β + β + γ = 90 => γ = −90 <−−−− sprzeczne
c.n.d.
11 lut 14:00
pigor: hmm..., otóż ...

spójrzmy na czworokąt ACDE i jego przekątne AD i CE ,
|∡ADC|=|∡CEA|=90
o kąty proste oparte na średnicy AC okręgu o środku w połowie
AC opisanego na tym czworokącie, a to oznacza, że
|∡ACD| + |∡AED| = 180
o ,
ale także
|∡BED| + |∡AED| =180
o − jako kąty przyległe , więc
|∡ACD| =
∡ACB =
∡BED , a ponieważ
|∡ABC|=|∡|EBD| − jako kąty wspólne ,
stąd
ΔABC∼ ΔEBD − trójkąty
podobne cecha (
k k k ) . ...

11 lut 14:32

 W trójkącie ostrokątnym ABC z wierzchołków A i C opuszczono wysokości AD i CE na boki BC i AB.
Wykaż, że trójkąty ABC i BDE są podobne.
W końcowej fazie zostaje mi trójkąt i nie potrafię jego kątów uzależnić od reszty kątów prze
zemnie wyliczonych... Jak wprowadzę dwa dodatkowe oznaczenia to wychodzi błędne kolo...
W trójkącie ostrokątnym ABC z wierzchołków A i C opuszczono wysokości AD i CE na boki BC i AB.
Wykaż, że trójkąty ABC i BDE są podobne.
W końcowej fazie zostaje mi trójkąt i nie potrafię jego kątów uzależnić od reszty kątów prze
zemnie wyliczonych... Jak wprowadzę dwa dodatkowe oznaczenia to wychodzi błędne kolo...


 Tak naprawdę to zadanie polega na udowodnieniu, że tak skonstruowany odcinek DE jest || do AC.
Tak naprawdę to zadanie polega na udowodnieniu, że tak skonstruowany odcinek DE jest || do AC.
 ... a oczywiśce nie jest ...
... a oczywiśce nie jest ...
 ?
?

 ? ...
? ...
 nic więcej nie ma w zadaniu
nic więcej nie ma w zadaniu 

 Rysunek ... baaaardzo duży powinien być
Rysunek ... baaaardzo duży powinien być  Z ΔACD mam, że α+β+γ = 90o
Wtedy patrząc na ΔACE wiem, że nad β także jest kąt γ
Punkt przecięcia się prosty nazywam 'S'.
ΔCSD podobny do Δ ASE (te same kąty).
na niebiesko podaję długości odcinków.
nazielono szukane kąty
ΔACE podobny do ΔSCF.
ΔDAC podobny do ΔFAS.
....
Z ΔACD mam, że α+β+γ = 90o
Wtedy patrząc na ΔACE wiem, że nad β także jest kąt γ
Punkt przecięcia się prosty nazywam 'S'.
ΔCSD podobny do Δ ASE (te same kąty).
na niebiesko podaję długości odcinków.
nazielono szukane kąty
ΔACE podobny do ΔSCF.
ΔDAC podobny do ΔFAS.
....
 patrzę na ten czworokąt.
fioletowe oznaczenia są to miary kątów.
Z podobieństw, które zapisałem wcześniej mam:
patrzę na ten czworokąt.
fioletowe oznaczenia są to miary kątów.
Z podobieństw, które zapisałem wcześniej mam:
 spójrzmy na czworokąt ACDE i jego przekątne AD i CE ,
|∡ADC|=|∡CEA|=90o kąty proste oparte na średnicy AC okręgu o środku w połowie
AC opisanego na tym czworokącie, a to oznacza, że |∡ACD| + |∡AED| = 180o ,
ale także |∡BED| + |∡AED| =180o − jako kąty przyległe , więc
|∡ACD| = ∡ACB = ∡BED , a ponieważ |∡ABC|=|∡|EBD| − jako kąty wspólne ,
stąd
ΔABC∼ ΔEBD − trójkąty podobne cecha (k k k ) . ...
spójrzmy na czworokąt ACDE i jego przekątne AD i CE ,
|∡ADC|=|∡CEA|=90o kąty proste oparte na średnicy AC okręgu o środku w połowie
AC opisanego na tym czworokącie, a to oznacza, że |∡ACD| + |∡AED| = 180o ,
ale także |∡BED| + |∡AED| =180o − jako kąty przyległe , więc
|∡ACD| = ∡ACB = ∡BED , a ponieważ |∡ABC|=|∡|EBD| − jako kąty wspólne ,
stąd
ΔABC∼ ΔEBD − trójkąty podobne cecha (k k k ) . ... 