Studentka: Na płaszczyźnie zespolonej naszkicuj zbór A = { z ∊ Complex : Re(z2 − 3) > O ∧ | z/(z+1| < 1 Wrzucam kolejne zadanie może tym razem ktoś pomoże

Studentka: znajdzie ktoś czas dla mnie? jutro zaliczenie, a ja wciąż mam braki

Studentka: wrzucam jeszcze raz treść, tylko ładniej przepisaną Na płaszczyźnie zespolonej naszkicuj zbiór: A = { z ∊ Complex : Re(z² − 3) > 0 ∧ | z / (z + 1) | < 1 }

ZKS: z = x + iy Re((x + iy)² − 3) > 0 Re(x² − y² + 2ixy) − 3 > 0 x² − y² − 3 > 0 ⇒ −√x² − 3 < y < √x² − 3

	z
|		| < 1
	z + 1

|z| < |z + 1| √x² + y² < √(x + 1)² + y² x² + y² < (x + 1)² + y² 2x > 1

	1
x >
	2

Teraz to narysować na płaszczyźnie i zaznaczyć część wspólną.

Studentka: rozumiem że 2ixy opuszczamy bo chodzi jedynie o cześć rzeczywistą, tak? a jak narysować tą pierwszą część? Bo jakoś nie mam pomysłu

Studentka: Uprzedam że ciężkawy ze mnie przypadek

Grześ: Masz dwa ramiona paraboli Tylko że zorientowane względem osi OX

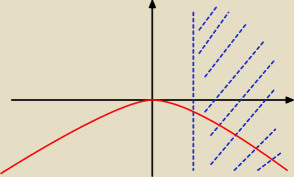
Studentka: chodzi o coś takiego? wstyd mi, ale te blond włosy chyba jednak mają czasem coś prawdy w sobie

ZKS: A wiesz jak narysować −√x² − 3 i √x² − 3 ?

ZKS: Nie w tą stronę będziesz miała tą parabolę Grześ napisał że względem OX.

Grześ: pomyliło mi się.. ech... to bedzie troszkę inaczej wygięta krzywa Późna pora i zobaczyłem kwadraty, więc od razu parabola To będzie wykres względem osi OX od (−∞,−√3>U<√3,+∞) i w nieskonczonościach zbliżający się do linii prostej y=x

Grześ: ważne, żebyś te początki krzywej dość dokładnie, starannie naszkicowała.. potem wykres zbliża się wartościami do prostej

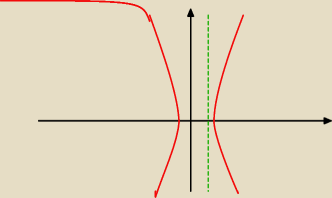
Studentka: nie linczujcie mnie, ale czy chodzi o coś takiego? i hiperbola przecina się w punkcie 3 i −3 z osią oX nie wiem dlaczego tam na górze tak dziwnie pokazuje, ale mniejsza z tym

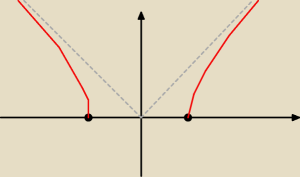
Grześ: Coś takiego

Grześ: te punkty to −√3 i √3

ZKS: Grześ jeszcze zapomniałeś o dolnych ramionach chyba że tylko rysowałeś √x² − 3 bez −√x² − 3.

Studentka: czyli mój rysunek by przeszedł na ogół?

ZKS: Tak. Tylko że ta hiperbola przecina się z osią OX w punkcie x = ±√3 a nie 3 ale rysunek dobry.

Studentka: A mogę zadać jeszcze jedno głupie pytanie? Bo wszystko rozumiem, ale mam problem dlaczego w momencie kiedy mamy x² − y² −3 > 0 nagle skupiamy się na y i robimy −√x²−3 < y √x²−3 pierwiastek rozumiem że po to, aby ściągnąć potęgę z y i x, ale dlaczego akurat y, a nie x? chociaż i w drugim zadaniu zauważyłem że |z + 1| traktuje się jak √(x+1)² + y²

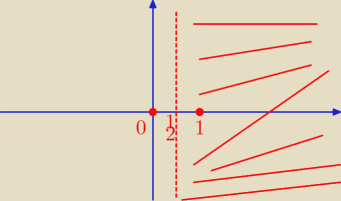
Godzio: Wtrącę się, |z| < |z + 1| Odległość od punktu (0,0) jest mniejsza od odległości od punktu (1,0) (wszystko na płaszczyźnie zespolonej) −− rozwiązaniem jest półpłaszczyzna, począwszy od symetralnej tego odcinka Chodzi mi o to, że nie trzeba rozbijać z na x + yi

Godzio: A i na 1 powinno być kółeczko otwarte bo ten punkt nie należy do rozwiązania

Studentka: OSTATNI RAZ ZAWRACAM GŁOWĘ! obiecuję możecie mi sprawdzić to zadanko? męczę je już któryś raz i ciągle wychodzą mi inne wyniki, a powinno wyjść co innego może gdzieś popełniam ten sam błąd? http://img836.imageshack.us/img836/6810/img9053m.jpg

Trivial: http://www.wolframalpha.com/input/?i=inv{{-3%2C1}%2C{2%2C-2}}+*+{{1%2C2}%2C{3%2C4}}+*+inv{{4%2C2}%2C{5%2C1}}

mać: Re(x−iy)³>=0 prosze o pomoc