Na prostej y-x-1=0 znaleźć punkt A taki, by pole trójkąta o wierzchołkach A,B=(4
Monika: Na prostej y−x−1=0 znaleźć punkt A taki, by pole trójkąta o wierzchołkach A,B=(4,−1) i C=(4,3)
bylo
rowne 2
Z góry dziekuje za pomoc

10 lut 19:43
Bizon:
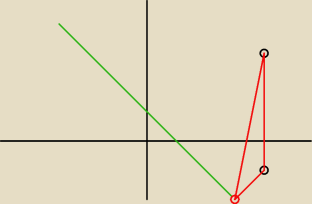
10 lut 19:50
Monika: Prosiłabym w miare mozliwosci rownież o wytlumaczenie

10 lut 19:51
Krzysiek: Bizon, z tego co widzę, y=x+1 ..
a u Ciebie to zielona funkcja to przypomina: y=−x+1
Monika, |BC|=4
więc odległość punktu A(a,b) od prostej x=4, musi być równa 1
Skorzystaj ze wzoru na odległość, punktu od prostej i z tego, że:
a−b−1=0 (ponieważ, punkt A należy do tej prostej )
10 lut 19:57
Bizon:
.. oczywiście masz rację ...
10 lut 19:59
Gustlik:
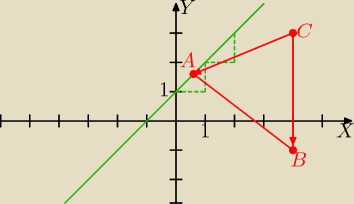
y=x+1
B=(4,−1)
C=(4,3)
A=(x, x+1)
Z wyznacznika wektorów − za początek wybiorę sobie punkt C, żeby jeden wektor (CB
→) miał znane
współrzędne, będzie łatwiej wtedy liczyć.
Liczę współrzędne wektora CB
→=B−C=[4−4, −1−3]=[0, −4]
Liczę współrzędne wektora CA
→=A−C=[x−4, x+1−3]=[x−4, x−2]
Liczę wyznacznik tych wektorów:
d(CB
→, CA
→)=
| 0 −4 |
| x−4 x−2 |
=0*(x−2)−(−4)*(x−4)=4x−16
| | 1 | |
Pole = |
| |d(CB→, CA→)|=2 |
| | 2 | |
|4x−16|=4 /:4
|x−4|=1
x=4+1 v x=4−1
x
1=5 v x
2=3
y=x+1 (punkt A leży na prostej o tym równaniu)
y
1=6 v y
2=4
Zatem:
A
1=(5, 6) v A
2=(3, 4)
[P[Opis wektorowej metody obliczania pól figur jest tutaj

]
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 .
11 lut 01:33



 y=x+1
B=(4,−1)
C=(4,3)
A=(x, x+1)
Z wyznacznika wektorów − za początek wybiorę sobie punkt C, żeby jeden wektor (CB→) miał znane
współrzędne, będzie łatwiej wtedy liczyć.
Liczę współrzędne wektora CB→=B−C=[4−4, −1−3]=[0, −4]
Liczę współrzędne wektora CA→=A−C=[x−4, x+1−3]=[x−4, x−2]
Liczę wyznacznik tych wektorów:
d(CB→, CA→)=
| 0 −4 |
| x−4 x−2 |
=0*(x−2)−(−4)*(x−4)=4x−16
y=x+1
B=(4,−1)
C=(4,3)
A=(x, x+1)
Z wyznacznika wektorów − za początek wybiorę sobie punkt C, żeby jeden wektor (CB→) miał znane
współrzędne, będzie łatwiej wtedy liczyć.
Liczę współrzędne wektora CB→=B−C=[4−4, −1−3]=[0, −4]
Liczę współrzędne wektora CA→=A−C=[x−4, x+1−3]=[x−4, x−2]
Liczę wyznacznik tych wektorów:
d(CB→, CA→)=
| 0 −4 |
| x−4 x−2 |
=0*(x−2)−(−4)*(x−4)=4x−16
 ] https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 .
] https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 .