planimetria
Ania: Uzasadnij, że jeśli w trapez prostokątny ABCD można wpisać okrąg to trójkąt, którego
wierzchołkami są środek O okręgu i końce dłuższego ramienia, jest prostokątny.
prosze o pomoc

Gustlik:

Ta reguła dotyczy wszystkich trapezów, w które można wpisać okrąg.
Środek okręgu wpisanego w dowolny wielokąt, w który można wpisać okrąg, leży zawsze w punkcie
przecięcia się dwusiecznych wszystkich kątów tego wielokąta.
Niech |∡A|=2α, |∡B|=2β, |∡C|=2γ, |∡D|=2δ, przy czym kąty A, B, C, D to kąty trapezu leżące przy
odpowiednich wierzchołkach.
Z własności trapezu wiadomo, że suma kątów utworzonych przez ramię trapezu z jego podstawami
jest równa 180
o (katy przyległe i odpowiadające).
Zatem:
|∡A|+|∡D|=2α+2δ=180
o, czyli α+δ=90
o, z sumy kątów ΔAOD wynika, że ∡AOD=180
o−(α+δ)=90
o,
czyli ΔAOD jest prostokątny.
W analogiczny sposób można udowodnić, że ΔBOC jest również prostokątny udowadniając, że
β+γ=90
o.
Własność ta dotyczy również trapezów prostokątnych, w tym także ramienia prostopadłego do
podstaw trapezu prostokątnego.
Jest to bardzo ciekawa własność, nie raz ją wykorzystywałem w zadaniach, bo ułatwiała ona ich
rozwiązanie, mozna np. wykorzystać twierdzenie Pitagorasa oraz pozostałe własności trójkątów
prostokątnych utworzonych "na ramionach" trapezu.

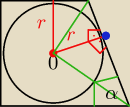 niebieski pkt to punkt stycznosci zielone to dwusieczne a czerwone to promienie. tylko nie wiem
co dalej ?
niebieski pkt to punkt stycznosci zielone to dwusieczne a czerwone to promienie. tylko nie wiem
co dalej ?
 Ta reguła dotyczy wszystkich trapezów, w które można wpisać okrąg.
Środek okręgu wpisanego w dowolny wielokąt, w który można wpisać okrąg, leży zawsze w punkcie
przecięcia się dwusiecznych wszystkich kątów tego wielokąta.
Niech |∡A|=2α, |∡B|=2β, |∡C|=2γ, |∡D|=2δ, przy czym kąty A, B, C, D to kąty trapezu leżące przy
odpowiednich wierzchołkach.
Z własności trapezu wiadomo, że suma kątów utworzonych przez ramię trapezu z jego podstawami
jest równa 180o (katy przyległe i odpowiadające).
Zatem:
|∡A|+|∡D|=2α+2δ=180o, czyli α+δ=90o, z sumy kątów ΔAOD wynika, że ∡AOD=180o−(α+δ)=90o,
czyli ΔAOD jest prostokątny.
W analogiczny sposób można udowodnić, że ΔBOC jest również prostokątny udowadniając, że
β+γ=90o.
Własność ta dotyczy również trapezów prostokątnych, w tym także ramienia prostopadłego do
podstaw trapezu prostokątnego.
Jest to bardzo ciekawa własność, nie raz ją wykorzystywałem w zadaniach, bo ułatwiała ona ich
rozwiązanie, mozna np. wykorzystać twierdzenie Pitagorasa oraz pozostałe własności trójkątów
prostokątnych utworzonych "na ramionach" trapezu.
Ta reguła dotyczy wszystkich trapezów, w które można wpisać okrąg.
Środek okręgu wpisanego w dowolny wielokąt, w który można wpisać okrąg, leży zawsze w punkcie
przecięcia się dwusiecznych wszystkich kątów tego wielokąta.
Niech |∡A|=2α, |∡B|=2β, |∡C|=2γ, |∡D|=2δ, przy czym kąty A, B, C, D to kąty trapezu leżące przy
odpowiednich wierzchołkach.
Z własności trapezu wiadomo, że suma kątów utworzonych przez ramię trapezu z jego podstawami
jest równa 180o (katy przyległe i odpowiadające).
Zatem:
|∡A|+|∡D|=2α+2δ=180o, czyli α+δ=90o, z sumy kątów ΔAOD wynika, że ∡AOD=180o−(α+δ)=90o,
czyli ΔAOD jest prostokątny.
W analogiczny sposób można udowodnić, że ΔBOC jest również prostokątny udowadniając, że
β+γ=90o.
Własność ta dotyczy również trapezów prostokątnych, w tym także ramienia prostopadłego do
podstaw trapezu prostokątnego.
Jest to bardzo ciekawa własność, nie raz ją wykorzystywałem w zadaniach, bo ułatwiała ona ich
rozwiązanie, mozna np. wykorzystać twierdzenie Pitagorasa oraz pozostałe własności trójkątów
prostokątnych utworzonych "na ramionach" trapezu.