proszę o pomoc bjorg: Wyznacz przedzialy monotoniczności i ekstrema funkcji: f(x)= (x + 4)e^3x

jo: Oblicz pierwsze pochodną tej funkcji.

bjorg: f'(x)= e^3x + (x + 4) e^3x

jo: Zapomniałeś/aś trójki: e^3x + 3(x+4)e^3x Teraz znajdź dla jakich x f'(x)=0, f'(x)>0 oraz f'(x)<0

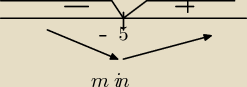
Aga1: f^'(x)=0 e^3x(x+5)=0 e^3x=0 lub x+5=0 brak pierwiastków x=−5 f(x) jest rosnąca dla x∊(−5,∞), a malejąca (−∞,−5) y_min=f(−5)=−e⁻¹⁵.

Aga1:

	−13
Faktycznie brak 3, więc zmieni się: nie x= −5 lecz x=		.
	3

Wszystko trzeba pozmieniać.

bjorg: A dlaczego 3 jest przed nawiasem?

jo: (e^3x)' = 3e^3x