Czworokąty - trapez.
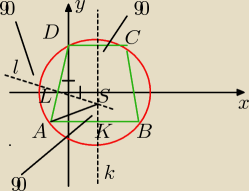
Hiromi_Ise: Punkty A, B, C, D, gdzie A = (−2,−3), B = (6,−3), C = (4,3), D = (0,3) są wierzchołkami trapezu
równoramiennego. Oblicz współrzędne środka okręgu opisanego na tym samym trapezie oraz promień
tego okręgu.
Rozwiązanie. Zauważamy, że środek S okręgu o promieniu R, opisanego na trapezie ABCD, jest
punktem przecięcia się symetralnych jego boków, np. boków AB i AD.
− symetralna k boku AB jest prostopadła do osi x oraz przechodzi przez punkt K, gdzie K = (2,
−3), więc jej równanie ma postać x = 2.
− Symetralna l boku AD przechodzi przez jego środek L, gdzie L = (−1,0), i jego prostopadła do
prostej AD.
| | yD − yA | |
Z warunku ml * mAD = −1. gdzie mAD = |
| = 3, wynika, że |
| | xD − xA | |
| | 1 | | 1 | |
Zatem y − yL = ml(x − xL) , czyli y − 0 = − |
| (x + 1), więc y = − |
| x − |
| | 3 | | 3 | |
− Obliczamy współrzędne środka S okręgu.
x = 2
y = −1
− obliczamy promień R okręgu
R = |AS| = 2
√5
Nie rozumiem tego zadania od drugiej pauzy i nie wiem o co chodzi z tym warunkiem. Ktoś pomoże?
(zaraz dorzucę rysunek)