Układy równań liniowych. Studentka : Witam mam taki układ równań. 2x + y − 3t = −1 −x + y + t = 2 −x + 4y = 5 Wyznacznik =0, a rząd = 1 więc co w takiej sytuacji ? metodą Cramera tego nie policzę,a Capellego nie bardzo wiem jak

Godzio: Rząd jest 2, policz rząd macierzy uzupełnionej

Godzio: Rząd macierzy jest 2, rząd macierzy uzupełnionej też jest 2, zatem mamy jedno parametrową rodzinę rozwiązań: x = 4t − 3 y = 2 − t t ∊ R Ja bym to tak zrobił

Studentka : jak rząd = 2 ? mi wychodzi 1 cały czas, a macierzy uzupełnionej to jakieś głupoty

Studentka : a może mi ktoś powiedzieć jak policzyć ten rząd ?

Godzio: Liczysz minorami czy metodą schodkową ?

Studentka : liczyłam tak zwaną metodą :"zerowania:" jednej kolumny lub wiersza, ale tą metodą wychodzi mi 1

Godzio: No to schodkowa, z niej wychodzi, że jest 2

Studentka : o.O ale jak, ale na wykładach mieliśmy jeszcze inną metodę ale tej nie rozumiem kompletnie... jak to policzyłeś ... ? Pomóż proszę bo w sobotę mam poprawkę z matmy

Godzio: 2 1 −3 | −1 −1 1 1 | 2 −1 4 0 | 5 w₁ + w₂ w₃ − w₂ 1 2 −2 | 1 −1 1 1 | 2 0 3 −1 | 3 w₂ + w₁ 1 2 −2 | 1 0 3 −1 | 3 0 3 −1 | 3 Widzimy, że w₂ = w₃, zatem możemy jeden wykreślić: 1 2 −2 | 1 0 3 −1 | 3 I widać, że rząd jest 2, więc możemy wyliczyć rozwiązania: x + 2y − 2t = 1 3y − t = 3 x + 2y − 2t = 1 y + t = 2 ⇒ y = 2 − t ⇒ x = 4t − 3, t ∊ R

Studentka : no dobra, ale ja to inaczej zerowałam troszeczkę... i zawsze taką metodę mogę zastosować ? i po czym ti widać że że rząd jest =2 ?

Godzio: Oj widzę, że na końcu zrobiłem błąd, odjąłem równania, a nie uwzględniłem x, zatem trzeba normalnie y wyliczyć i podstawić do 1 równania

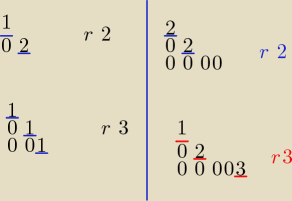
Godzio: Po tym, oczywiście bez różnicy czy jest tam 1 czy nie, w każdym razie nie może być 0 Narysowałem kilka przykładów

Studentka : czyli tu chodzi o to że jest bo jest to 1 i 3 tak ?

Godzio: Tak, tylko trzeba pamiętać, że w dół od 1 muszą iść same 0

Godzio: Dobra to dla ćwiczeń podaj rzędy takich macierzy: 1 2 1 1 3 2 2 2 5 1 2 2 0 3 1 0 4 1 1 3 2 1 4 5 0 1 3

Studentka : ale ten pierwszy to coś nie tak na minusie powinno coś być

Godzio: Czemu ? Wymyśliłem je sobie, podaj wyniki jakie Ci wychodzą, o ile wychodzą ?

Studentka : aha ... xD niestety żadne mi nie wyszło 1. 2 5 1 1 3 2 1 1 3 2. 2 7 5 1 5 3 0 1 0

Godzio: Oj to źle, W pierwszym: w₂ − w₁ w₃ − 2w₁ ZAPISZ WYNIK w₁ − w₂ w₃ + 2w₂ ZAPISZ WYNIK I PODAJ ODP R = 3 Drugie: w₃ − w₂ w₁ − w₂ ZAPISZ WYNIK

	1
w3 −		w2
	3

ZAPISZ WYNIK I PODAJ ODP R = 3 Trzecie: w₂ − w₁ PODAJ WYNIK I ZAUWAŻ COŚ R = 2 Działaj, ja wracam za moment i oczekuje rozwiązań

Studentka : ale jak ? coś to nie jasne dla mnie jest dlaczego teraz dla pierwszego ma być w₂ − w₁ w₃ − 2w₁ < −−− co to jest to 2 ? nie ma takiej metody gdzie wszędzie jest to samo zastosowanie ?

Godzio: No to zerowanie stosuje się wszędzie , w₃ − 2w₁ ⇒ od wiersza 3 odejmij dwa razy wiersz pierwszy

Studentka : a patrz ja robiłam tak 2 1 −3 −1 1 1 −1 4 0 zeruje kolumnę 3 bo mam tam 0 już jedno i 1 ( a z jedynka najprościej się zeruje) czyli tak: wiersz 2 dodam do 1 ale muszę to jeszcze przemnożyć przez taką liczbą żeby z −3 wyszło 0. więc wyjdzie tak −1 4 0 −1 1 1 −1 4 0 i z tego co mi wyszło wykreślam kolumne i wiersz gdzie jest ta 1 i 0 i robię tak 1 + | −1 4 −1 4| = 1 + 0 bo tą macierz licze na skos −1*4 − (−1)*4 i wychodzi 1 1+

Studentka : ale ja wyznacznik w macierzy wychodzi 0 to rząd automatycznie jest = 1 tak ma zapisane w każdym bądź razie

Godzio: Dobra wiesz co, jak chcesz, żebym Ci pomógł to jakoś bardzo wieczorem będę mógł coś posiedzieć, teraz mam korepetycje, więc muszę uciekać, a z tego co widzę, to Ty masz minory, a nie zerowanie ... Więc się nie dogadaliśmy

Studentka : a o której tak mniej więcej ?

Godzio: Bardziej 21:30 i później Może ktoś się znajdzie kto Ci teraz pomoże,

Studentka : dobra to jak dasz rade to bądź bo musze się tego nauczyć z góry dzięki

Studentka : up up up podnoszę ... jest ktoś kto mi to wytłumaczy ?

Godzio: Dobra to lecimy

Studentka : o jesteś to od początku najlepiej

Godzio: 2 1 −3 −1 1 1 −1 4 0 Rząd tej macierzy jest maksymalnie 3, to jest jasne, kiedy będzie 3 ? Ano wtedy kiedy wyznacznik 3x3 będzie różny od 0, sprawdzamy: w₁ + 3w₂ −1 4 0 −1 1 1 −1 4 0 Rozwijamy Laplace'em względem 3 kolumny:

	⎧	− 1 4
(−1)2 + 3 *	⎩	−1 4	= − 1 * (−4 + 4) = 0

Zatem macierz nie jest rzędu 3, szukamy dowolnego niezerowego minora stopnia 2, weźmy chociażby ten: 4 0 1 1 Jego wyznacznik jest równy 4, zatem rząd tej macierzy jest 2

Studentka : dobra to tak: najpierw liczymy wyznacznik tak ? jeśli jest różny od 0 i wynosi np 7 do rzad macierzy jest równy 2 lub 3 ? niestety mam tylko szczątkowe informacje a szanowny doktor nie raczy tego wytłumaczyć .. a metodzie Leplaca nawet nie słyszałam ...

Godzio: No to się nie przejmuj, wystarczy policzyć ten wyznacznik, Sarrusem chociażby Tzn tak, mamy macierz, ustalamy jej maksymalny rząd (jaki może mieć) i liczymy wyznacznik takiej macierzy jakiej przypuszczamy, że będzie rząd Przykładowo mamy macierz 4 x 3, jej maksymalny rząd to 3, zatem liczymy wyznacznik 3x3 składający się z 3 dowolnych wierszy jeśli wyjdzie ≠ 0 to rząd takowej macierzy jest 3, jeśli nie to liczymy dalej (musimy zbadać wszystkie możliwe wyznaczniki 3 x 3) jeśli okrze się, że wszystkie te wyznaczniki są równe 0 to nie ma szans na r = 3, więc liczymy 2 x 2, jeśli trafimy na choćby jeden niezerowy wyznacznik to już wiemy, że rząd jest równy 2

Studentka : albo zrobić tak że np policzę wyznacznik z tego jak wyjdzie mi różny od zera to biorę np −1 4 −1 4 i licze z tego rząd albo coś ?

Studentka : o widzisz ...i to zawsze moge zastosować ? w każdym przypadku się sprawdzi ?

Godzio: Jak weźmiesz taki minor z Twojej macierzy i policzysz jego wyznacznik to on wychodzi 0 prawda ? Więc szukasz dalej takiego wyznacznika, żeby się nie zerował, dopóki takiego nie znajdziesz musisz liczyć (wystarczy, że jeden się nie zeruje i już mamy rząd odpowiadający wielkości tego minoru )

Godzio: W każdym

Studentka : a czemu mionry się to zwie ? tak poza konkursem pytanie

Studentka : np mam taką macierz −1 4 5 6 2 3 −4 2 1 tu rząd maksymalnie może być 3 więc liczę wyznacznik, który równa się 32 jest ≠0 więc rząd jest różny 3 ?

Godzio: Rząd jest równy 3 (pewnie pomyłka w pisaniu )

Studentka : tak tak czyli tak to wyjdzie ? to daj 5 min ja policzę sobie rząd z mojego zadania na samym początku co podawałam bo tam mi 0 wyszło ...

Godzio: Ok

Godzio: Ale to jak 0 to dobrze Ci wychodziło Tylko Ty napisałaś, że r = 1, a trzeba było policzyć jeszcze wyznacznik 2 x 2 i pokazać, że r = 2

Studentka : dobra to tam z każdej kombinacji macierzy 2x2 wychodzi wyznacznik różny od 0 więc macierz jest rzędu 2

Studentka : no właśnie bo jak jest macierz 2x2 i wyznacznik z niej wychodzi 0 to rząd jest równy 1 taka jest niby zasada

Studentka : ale wracając do tego zadania NIE JEST to układ Cramera więc wg moje wykładowcy powinnam to policzyć metodą Capellego a tam Rząd macierzy A powinien być równy rzędowi macierzy Uzupełnionej A co jeśli nie jest ?

Godzio: ZAPAMIĘTAJ WYSTARCZY, ŻE JEDEN WYZNACZNIK 2 X 2 BĘDZIE RÓŻNY OD 0 I JUŻ MASZ RZĄD DWA

Godzio: Jeśli nie jest to mamy układ sprzeczny

Studentka : dobra to tam macierz uzupełniona wychodzi 3x4 to jak mam wyznacznik policzyć ?

Godzio: Przeczytaj post z 21:44 UWAŻNIE I pomyśl

Studentka : ale jeśli dobrze obstawiam to rząd macierzy uzupełnionej tam też jest =2 : D

Godzio: No zgadza się, ale powiedz co trzeba policzyć, żeby to pokazać

Studentka : czyli wybieram 3 dowolne kolumny ... ja wybrałam tą z wyrazów wolnych z niewidomych t i y wyznacznik wyszedł =0 ale wyznacznik macierzy 2x2 wyszedł ≠0 więc rząd jest równy 2

Godzio: Musisz sprawdzić WSZYSTKIE 3x3 i jeśli wszystkie się zerują to rząd < 3

Studentka : ale 3x3 się zerują bo macierz uzupełniona to jest ta sama co macierz nie uzupełniona i obie się zerują ... o to chodzi ?

Godzio: 2x + y − 3t = −1 −x + y + t = 2 −x + 4y = 5 Mamy zatem macierz: 2 1 − 3 −1 −1 1 1 2 −1 4 0 5 Liczymy wyznaczniki: 2 1 −1 −1 1 2 −1 4 5 1 − 3 − 1 1 1 2 4 0 5 2 − 3 −1 −1 1 2 −1 0 5 Jeśli wszystkie się zerują, to sprawdzamy 2 x 2 jeśli znajdziemy jeden niezerowy to już mamy rząd 2

Studentka : aha to tak trzeba to układać a mogę po prostu wyrazami wolnymi zastępować kolejno kolumnę x, y i t ?

Godzio: Hmmm, nie jestem pewien czy zamiana kolumn nie zmienia przypadkiem wartości wyznacznika, nie pamiętam, trzeba by sprawdzić

Studentka : bo generalnie w tym co ty wypisałaś za każdym razem brakuje jednej kolumny. Ale wyrazy wolne są zawsze na końcu i tego się lepiej trzymać ?

Studentka : no i z tego co wypisałeś ten środkowy się nie zeruje więc Rząd =2

Godzio: Wartość jest inna, co prawda tylko znak −/+ się zmienia, ale lepiej nie ryzykować z kombinowaniem

Godzio: Wszystkie się zerują

Studentka : czyli lepiej trzymać się Twojej metody ... no to ok czyli tak I warunek do rozwiązania równania metodą Capellego jest i co dalej ?

Studentka : jak ?

Studentka : mi wyszło −5

Godzio: Dlatego rząd nie jest 3. Teraz sprawdzamy dowolny 2 x 2 i któryś się nie zeruje to rząd jest 2

Godzio: To policz jeszcze raz

Studentka : fuck błąd w obliczeniu

Studentka : 2 1 −1 1 z tego wychodzi 3, wiec rząd jest równy 2 ?

Godzio: Tak

Studentka : czyli układ sprzeczny

Studentka : ale co jeśli Rząd macierzy A = Rzędowi macierzy Uzupełnionej ? Jak to liczyć ?

Godzio: Liczba parametrów = Liczba niewiadomych − Rząd p = 3 − 2 = 1 Zatem u Ciebie mamy jeden parametr, przyjmujemy, że jest to t ∊ R i teraz musisz wyliczyć x i y

Godzio: Sposób taki jak podałem na początku, po odpowiednim przekształceniu widzimy, że pozostaje nam: x + 2y − 2t = 1 3y − t = 3 ⇒ y = ... Wstawiamy danego y do pierwszego równania i wyliczamy x Odpowiedź podajemy w taki sposób:

⎧	x = ...
⎨	y = ...
⎩	t∊R

Studentka : ale to jak układ nie jest sprzeczny ? w tym co ja podałam ?

Godzio: Nie

Studentka : fuck this i tak pewnie nie zdam ...

Godzio: Jeśli mamy, że r(M) < r(M_u) to wtedy mamy sprzeczność, czytaj moje wpisy uważnie, nie lubię się powtarzać, a już to kilka razy robiłem

Studentka : ale wiesz co jest najgorsze ... ? że ja już nie pamiętam jak to liczyć muszę zacząć wszystko notować.v

Godzio: ...

Studentka : wiem "bez komentarza", ale jednak nie przyswajam wiedzy tak jak miał lat 20 przeanalizuje sobie to sama jutro jeszcze i może dojde do sensownych wniosków a takim czymś jak przepływy międzygałęziowe słyszałeś ?

Godzio: Niestety nie

Studentka : dzięki wielkie za pomoc

Godzio: Nie ma sprawy Mam nadzieję, że te niecałe 3 h nie pójdą na marne

Studentka : up up up podnoszę mam taki układ równań −4x + 2y + t = 3 6x − 3y − 4t = 2 i wyszło mi że Rząd jest równy 2 i dalej ułożyłam taki układ równań 2y+t = 4x+3 −3y − 4t = −6x + 2 tylko jak to rozwiązać ?

Aga1: Obliczasz y i t , x traktujesz jako parametr.np metodą podstawiania czy przeciwnych współczynników układ ma nieskończenie wiele rozwiązań. np. za x=0, y= .... t=

Studentka : ale jak ? nic mi to nie mówi Aga1

Aga1: Zakładam, że dobrze wykonałaś wcześniejsze obliczenia. 2y+t=4x+3 //*4 −3y−4t=−6x+2 8y+4t=16x+12 −3y−4t=−6x+2 −−−−−−−−−−−−−−−− dodajemy stronami 5y=10x+14//:5

	14
y=2x+
	5

t=−2y+4x+3 z pierwszego równania

	14
t=−2*(2x+		)+4x+3
	5

i licz dalej.

Studentka : up up up ... mam problem z dziedziną funkcji jest ktoś kto pomoże ?