Planimetria
....: Zadanko z planimetrii jakby komuś się chciało
Z wierzchołka kąta rozwartego rombu opuszczono dwie prostopadle do jego boków. Długość każdej
prostopadłej jest równa a, zaś odległość między spodkami tych prostopadłych jest równa b.
Oblicz pole rombu.
9 lut 14:19
Kejt:
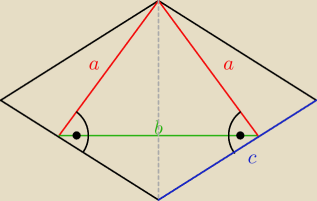
hmm chyba tak...trzeba jakoś ten bok 'c' wyznaczyć..muszę się jeszcze zastanowić..
a jak nie to może chociaż rysunek się przyda..
9 lut 14:45
....: wesprze ktoś radą?
9 lut 14:45
....: nom, rysunek już mam i pamiętam(kartkę mi gdzieś wcięło...), że ze cztery równanka ułożyłem, bo
cztery niewiadome wprowadziłem, ale obliczenia mnie zdemotywowały
9 lut 14:48
Kejt:
| | ac | |
i wtedy pole P= |
| *2=ac |
| | 2 | |
| | 2a2 | | a3 | |
czyli niby P=a* |
| = |
| |
| | b | | b | |
ale istnieje spore prawdopodobieństwo, że wyszło mi to z kosmosu..
9 lut 15:00
9 lut 15:03
....: nie jednak mniej tych niewiadomych wprowadziłem i wyglądało to u mnie następująco:
(
b2)
2+a
2=e
2−2ez+z
2 z−kawałek krótszej przekątnej od wierzchołka do odcinka b
x
2=z
2+(
b2)
2 x−kawalek dłuższej przekątnej od wierzchołka do odcinka a bodajże;
e
2=a
2+z
2+(
b2)
2
jak dobrze pamiętam
9 lut 15:11
Kejt: wiesz co..nie patrz lepiej na to
palnełam w jednym miejscu wielką gafę..
9 lut 15:13
....: ok, ale muszę Ci powiedzieć, że wynik bardzo ładnie się prezentował
byłbym skłonny w niego
uwieżyć
9 lut 15:15
Kejt: och, uznam to za komplement
zaraz może się uda uzyskać równie ładny tylko tym razem
prawdziwy
9 lut 15:16
Artur z miasta Neptuna:
tylko jedna sprawa −−− podstawa trójkąta ma długość 2b, a nie b (też na początku źle
zaznaczyłem)
9 lut 15:18
....: ok, też chwilę się zastanowię, może teraz mnie oświeci
9 lut 15:18
Kejt: Artur, o co dokładnie chodzi..? nie bardzo rozumiem..
9 lut 15:20
....: aha, czyli spodek to tak jakby pkt., w którym przekątna przecina ten odcinek b?
9 lut 15:20
Artur z miasta Neptuna:
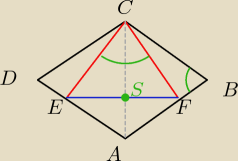
w treści jest podana długość 'b' jako odcinek łączący ŚRODKI tych wysokości, a nie ich końce
wtedy z tw. Talesa masz, że podstawa = 2b
ja mam taki pomysł:
∡ECF + ∡FCB = 90
o
∡FCB + ∡FCB = 90
o
=> ∡ECF = ∡FCB => ΔABC ∼ ΔFCE
także:
ΔCFA ∼ ΔCSF
i robię proporcje:
| d1 | | a | | a2 | |
| = |
| => d1 = |
| gdzie h = |CS| = √a2−b2 i d = |AC| |
| a | | h | | h | |
oraz
| x | | d1 | | d1*a | | a3 | |
| = |
| => x= |
| = |
| |
| a | | 2b | | 2b | | 2bh | |
| | a4 | |
Prombu = a*x = |
| ; gdzie h= √a2−b2 |
| | 2bh | |
9 lut 15:31
Kejt: taak..to ja się lepiej schowam
9 lut 15:32
Artur z miasta Neptuna:
a nie sorki ... było dobrze ... podstawa to 'b' a nie '2b', więc u mnie trzeba zrobić b =
9 lut 15:32
Artur z miasta Neptuna:
Błąd nr 2 (tylko w zapisie).
∡ECF + ∡FCB = 90o
∡ACF + ∡FCB = 90o
9 lut 15:33
Artur z miasta Neptuna:
a no i oczywiście x = |AB|, czyli bok rombu ( u Kejt 'c')
9 lut 15:36
....: Mala poprawka ∡FCB + ∡DCE = 90
o, a nie jak napisałeś "∡FCB + ∡FCB = 90
o", chyba
9 lut 15:37
Artur z miasta Neptuna:
∡FCB + ∡DCE = 90o −−− a w życiu.
powinno być
∡FBC + ∡FCB = 90o −−− ponieważ −−− czyli kąty w ΔCBF, gdzie ∡BFC jest kątem prostym.
9 lut 15:42
Artur z miasta Neptuna:
dobra jeszcze raz wszystko:
∡ECF + ∡FCB = 90o
∡FBC + ∡FCB = 90o
=> ∡ECF = ∡FBC => ΔABC ∼ ΔFCE
także (łatwiej to zauważyć):
ΔCFA ∼ ΔCSF
i robię proporcje:
| d | | a | | a2 | |
| = |
| => d = |
| gdzie h = |CS| = √a2−(b/2)2 i d = |AC| |
| a | | h | | h | |
oraz
| x | | d | | ad | | a3 | |
| = |
| => x= |
| = |
| |
| a | | b | | b | | bh | |
| | a4 | |
Prombu = a*x = |
| ; gdzie h= √a2−(b/2)2 |
| | bh | |
teraz chyba żadnych literówek nie ma
9 lut 15:46
....: jak na moje oko to się pomyliłeś, bo jeżeli ∡ECF + ∡FCB = 90o to ACF + ∡FCB = 90 jest nie
prawdą
9 lut 15:47
....: teraz będzie git
9 lut 15:49
Artur z miasta Neptuna:
Nigdy nie byłem dobry w opisywaniu kątów
9 lut 15:51
....: muszę więcej takich zadań porobić, bo będzie cienko na maturze...
Mam jeszcze kilka zań, pomorzesz?
9 lut 15:53
Artur z miasta Neptuna:
to dawaj
mam nadzieję, ze wszystko na 'jedno kopyto' czyli na zauważenie tw. Talesa
9 lut 15:54
Kejt: pff..to ja sobie idę.
9 lut 15:56
Artur z miasta Neptuna:
Kejt −−− ojjj zostań zostań
9 lut 15:57
Kejt: za późno..obraziłam się. <tupie nóżką>
a tak serio..znikam, bo na gitarę jadę.
9 lut 15:58
....: Wyznacz liczbę x tak, by w prostokącie o bokach 1 i x proste poprowadzone z przeciwległych
wierzchołków i prostopadle do przekątnej dzieliły ją na trzy części o równych długościach.
Wygląda na proste, ale w zapisie mi się zeruje
9 lut 15:58
....: sorry za ortografię, właśnie zauważyłem
BYKA 
9 lut 16:15
pigor: ... niech α − miara kąta między krótszą przekątną
e i prostopadłą a , to z warunków
zadania :
| | b | | √4a2−b2 | | a | |
sinα= |
| ⇒ cosα = √1−sin2α= |
| = |
| ⇒ a = e cosα ⇒ |
| | 2a | | 2a | | e | |
| | a | | 2a2 | |
e = |
| = |
| , analogicznie , jeśli |
| | cosα | | √4a2−b2 | |
| | a | | a | | 2a2 | |
d− dłuższa przekątna rombu , to sinα = |
| ⇒ d = |
| = |
| , |
| | d | | sinα | | b | |
więc
| | 1 | | 4a4 | |
Prombu= |
| ed = |
| − szukane pole rombu . ... |
| | 2 | | b√4b2−a2 | |
9 lut 16:18
....: Coraz lepiej
9 lut 16:20
Artur z miasta Neptuna:
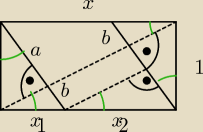
kąty na zielono są równe
d
1 = d
3 −−− to wiesz od początku (i będzie zawsze)
d
2 −−− środkowa część przekątnej
| | d1 | |
sin α = |
| (prawy trójkąt) |
| | 1 | |
| | 1 | |
sin α = |
| (duży trójkąt pod przekątną) |
| | d1+d2+d3 | |
skoro ma być d
1=d
2=d
3 to:
| | 1 | |
d1 = |
| => 3d12 = 1 => 9d12 = 3 |
| | 3d1 | |
z pitagorasa −−− (3d
1)
2 = x
2 + 1
2 => 3 = x
2 + 1 => x
2 = 2 => x=
√2
9 lut 16:24
Artur z miasta Neptuna:
pigor ... parę 'ale' do Twojego wyniku:
| | 1 | |
1. nie podzieliłeś przez |
| po podstawieniu przekątnych |
| | 2 | |
2. w pierwiastku powinno być 4a
2 − b
2 (jak miałeś wcześniej) a nie na odwrót
do autora −−− jeżeli uwzględni się te dwie rzeczy w wyniku pigora = mojemu
9 lut 16:28
....: Wydaje mi się, ze to x jest podzielone na trzy równe części, a nie d
9 lut 16:39
....: nie dobra wróć to jednak po głębszej analizie będzie przekątna. Źle zrozumiałem zadanie
9 lut 16:44
....: Dany jest rąb o boku a i kącie ostrym α. Romb ten podzielono na trzy części o równych polach
odcinkami mającymi wspólny początek w wierzchołku kata ostrego i końce w bokach rombu. Wyznacz
długości tych odcinków.
9 lut 16:48
Artur z miasta Neptuna:
r
ąb
9 lut 16:49
....: zauważyłem, niestety Ty też
Nie wiem, jak można napisać raz źle, a dwa razy dobrze w 4
zdaniach na krzyż?
9 lut 16:51
Artur z miasta Neptuna:
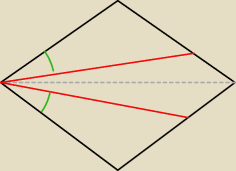
oczywistą oczywistością jest, że zielone kąty są sobie równe (tylko te same boki + 2 kąty
pozostałe + te same pola trójkątów)
wzór na pole rombu? P
rombu = a
2*sin α
| | a*b | |
wzór na pole trójkąta? Ptrójkąta = |
| sin β |
| | 2 | |
| | Pr | |
PΔ = |
| => 3b sinβ = 2a sinα |
| | 3 | |
i muszę pomyśleć.
9 lut 17:09
pigor: Artur−ze dziękuję , masz rację i przepraszam zainteresowanych, piszę online i nie lubię wracać
i szukać , co tam nabazgrałem . ...
9 lut 17:22
Artur z miasta Neptuna:
jeszcze doszedłem do tego ... że te odcinki dzielą bok rombu w stosunku 2:1 (krótsze stanowią
boki deltoidu, dłuższe trójkątów u góry i na dole).
9 lut 17:23
Artur z miasta Neptuna:
no i jasne ...
tw. cosinusów dla dolnego kąta (rozwartego)
| | 2a | | 2a | | 13a2 | | 12a2 | |
x2 = a2 + ( |
| )2 − 2a* |
| cos(180−α) = |
| + |
| cos α |
| | 3 | | 3 | | 9 | | 9 | |
9 lut 17:28
....: a wytłumacz mi jak doszedłeś do tego "że te odcinki dzielą bok rombu w stosunku 2:1"?
9 lut 17:38
....: jakby nie bylo to jest kluczowa informacja
9 lut 17:52
Artur z miasta Neptuna:
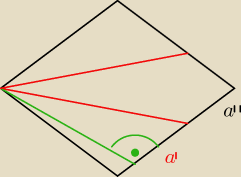
P
rombu = a*h ... gdzie h = zielona krecha
oraz
| | ah | | a'h | |
czyli |
| = |
| => 2a = 3a' |
| | 3 | | 2 | |
skoro a = a' + a'' to .... 2a' + 2a'' = 3a' −> a' = 2a''
| | a' | | 2 | |
czyli |
| = |
| ... tara |
| | a'' | | 1 | |
9 lut 17:59
....: ok, dzięki
To jedziemy dale jak Ci się nie znudziło
W trapezie opisanym na okręgu długości ramion są równe 3i 5. Odcinek łączący środki ramion
dzieli trapez na części, których pola są w stosunku 5:11. Oblicz długość podstaw trapezu
9 lut 18:26
Artur z miasta Neptuna:
korzystasz z dwóch twierdzeń:
1. Sumy przeciwległych boków (w czworokącie opisanym na okręgu) są sobie równe
czyli a+b = 3+5
| | a+b | |
2. długość odcinka łączącego środki boków trapezu wynosi |
| (i oczywiście dzieli |
| | 2 | |
wysokość trapezu na pół)
masz, że:
czyli:
5(a+8) = 11(b+8) => 5a = 11b + 48
i masz układ równań z niewiadomymi 'a' i 'b' (jedno z pola, drugie z 2.)
do dzieła
9 lut 18:41
....: a czyli jednak można
a+b2 użyć... Coś mi się ubzdurało, że tylko w równoramiennym
Żebyś nie wyszedł z formy już wrzucam następne
Trapez równoramienny o przekątnej 5cm i obwodzie 36cm jest opisany na okręgu. Oblicz dlugośc
promienia okręgu wpisanego w trapez i długość promienia opisanego na nim.
Tu mam mały problem, bo mi wychodzą wartości ujemne ...
c−ramię
b,a−krótsza, dłuższa podstawa
2c=a+b
2c+a+b=36
a=18−b
2c=18−b+a
c=9
2x−dwa odcinki równej długości przy podstawie
2x+b=a
x=
a−b2
x=
18−b−b2=9−b
(−b+9+b)
2+h
2=5
2
jak widać h wyjdzie ujemne i nie widzę błędu niestety
9 lut 19:05
Artur z miasta Neptuna:
jeszcze do poprzedniego
tam zamiast
5(a+8) = 11(b+8) => 5a = 11b + 48
powinno być:
5(a+4) = 11(b+4) => 5a = 11b + 24
teraz nowe
równoramienny więc:
2c = a+b
a+b+2c = 36 => a+b = 18 i c=9
przekątna = 5
przekątna
2 = (a−a')
2+h
2 => 5
2 = (a−a')
2+h
2
oraz
c
2 = a'
2+h
2 => 9
2 = a'
2+h
2
| | a−b | |
trzeba udowodnić, że a' = |
| (dotyczy tylko równoramiennego ... nie jest to trudne) |
| | 2 | |
no i masz układ 3 równań z trzema niewiadomymi (dwa pitagorasy oraz a+b =18)
stąd masz a,b,h
'r' −−− promień okręgu wpisanego w trapez
'R' −−− promień okręgu opisanego na trapezie
R −−− jakoś się oblicza (nie mam obecnie czasu nad ten temat myśleć).
9 lut 19:15
....: jak obliczę r to do R już dojdę
Dzięki wielkie za pomoc.
9 lut 19:35
10 lut 13:58
....: Witam ponownie. Teraz wyższa szkoła jazdy, bo same zadania typu wykaż.
ZADANIE
Wykaż, że w trójkącie prostokątnym suma kwadratów długości środkowych przyprostokątnych stanowi
54 kwadratu długości przeciwprostokątnej.
Oznaczyłem sobie te środkowe jako x(dłuższa), y(krótsza), z−przeciwprostokątna,
a−przeciwprostokątna krótsz b−dłuższa(podstawa)
x2=(a2)2+b2
y2=a2+(b2)2
z2=a2+b2
Teraz pytanie jak pozbyć się a i b tak, aby uzyskać te 54?
Próbowałem coś z tw. cosinusów, ale wyszło mi 2x2+2y2=z2 ...
10 lut 19:42
....: Jednak gdzieś się pomyliłem. To dobry sposób tylko bląd obliczeniowy jakiś mam. Teraz mi wyszlo
4y
2+4x
2=7z
2
10 lut 19:48
Kejt:
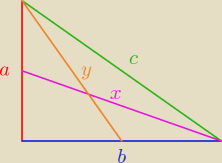
a
2+b
2=c
2
| | b2 | | a2 | | a2+b2 | |
y2+x2=a2+b2+ |
| + |
| =a2+b2 |
| = |
| | 4 | | 4 | | 4 | |
podstawiamy c
2 za a
2+b
2:
| | c2 | | 4c2 | | c2 | | 5 | |
=c2+ |
| = |
| + |
| = |
| c2 |
| | 4 | | 4 | | 4 | | 4 | |
10 lut 19:53
Kejt: c.n.u.
wystarczyło samo twierdzenie Pitagorasa
10 lut 19:54
....: kurde, a mi dalej wychodzi 4y
2+4x
2=7z
2
10 lut 20:01
Kejt: a podstawiłeś za y i x to co Ci z Pitagorasa wyszło?
w ogóle nie rozumiem po co Ci ta ostatnia linijka..
10 lut 20:04
....: Twoim sposobem policzyłem i wyszło
mój jest deczko dłuższy, ale też powinno wyjść to samo.
Musi być jakiś błąd obliczeniowy, ale go nie dostrzegam
Dasz się skusić na jeszcze kilka zadanek?
10 lut 20:10
Kejt: z chęcią.. nie mam co robić, a akurat powinnam poćwiczyć zadania z dowodami
10 lut 20:13
....: Długości dwóch boków trójkąta są równe 5 i 10. Wykaż, że długość odcinka będącego częścią
wspólną i dwusiecznej jego kąta wewnętrznego zawartego między bokami o podanych długościach
jest mniejsza od 20/3.
Za pierwszym razem wyszło mi wgl., że nie wychodzi trójkąt. Drugiego podejścia nie robiłem
10 lut 20:18
Kejt: długość odcinka będącego częścią wspólną..czego? bo nie rozumiem..
10 lut 20:21
....: Na moje oko to tu chyba trzeba obliczyć stosunek podstawy do odcinka będącego dwusieczną kąta
10 lut 20:33
....: Zdemotywowałaś się patrzę
10 lut 21:24
Kejt: niee..próbuję zrozumieć co to za część wspólna ma być..ale nie mam żadnego pomysłu
10 lut 21:25
....: ja też nie wiem
wyszedłem się przejść z kolegą i stwierdziłem, że strasznie zimno. Wracam do
domu, patrzę na termometr a tu −23
masz inne zadanko na rozluźnienie
W trójkącie ABC, gdzie |AC|=|BC|=
√10, środkowe poprowadzone z wierzchołków A oraz B
przecinają się pod kątem prostym Oblicz pole trójkąta
10 lut 22:05
....: Mam problem.
[P[ZADANIE]
Wykaż, że jeśli h jest dlugością wysokości trójkąta prostokątnego opuszczoną na jego
przeciwprostokątną, zaś a i b są długościami przyprostokątnych to
u[1}{h
2}=
1a2+
1b2.
| | ab | |
Zacząłem tak od porównania pól P=12ch i P=12ab => h= |
| =ab/√a2+b2 i nie wiem |
| | c | |
co dalej...?
10 lut 22:33
....: Ogarnę to co napisałem żeby dało się coś zobaczyć
ZADANIE Wykaż, że jeśli h jest długością wysokości trójkąta prostokątnego opuszczoną na
jego przeciwprostokątną, zaś a i b są długościami przyprostokątnych to
1h2=
1a2+
1b2.
Zacząłem tak od porównania pól P=1/2*ch i P=1/2*ab => h=
abc=ab/
√a2+b2
10 lut 22:51
pigor: ...
no to dalej
| | 1 | | √a2+b2 | | 1 | | a2+b2 | |
⇒ |
| = |
| ⇔ |
| =√ |
| ⇔ |
| | h | | ab | | h | | a2b2 | |
| 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
| =√ |
| + |
| ⇔ |
| = |
| + |
| − co należało wykazać . |
| h | | b2 | | a2 | | h2 | | b2 | | a2 | |
10 lut 23:26
...: kurde, liczyłem i nie wychodziło, jak zwykle gdzieś musiałem się walnąć...
Co mi na ten temat powiecie?
W trapezie ABCD łączymy środek M ramienia AB z końcami ramienia CD. Wykaż, że pole powstałego
trójkąta jest polową pola trapezu
10 lut 23:43
Artur z miasta Neptuna:
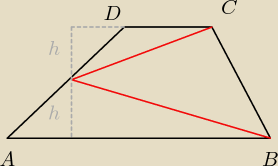
Zmieniłem podpisy trapezu na standardowe (AB i CD to podstawy a nie ramiona).
Skoro M to środek ramienia, to punkt M dzieli wysokość trapezu na dwa równe odcinki (H=h+h)
P
szukanego Δ = P
trapezu−P
ABM−P{CDM} =
| | (a+b)2h | | ah | | bh | | (a+b)h | |
= |
| − |
| − |
| = |
| = 1/2 Ptrapezu |
| | 2 | | 2 | | 2 | | 2 | |
Wykorzystałem fakt, że środek ramienia (a raczej równoległa do podstaw, przechodząca przez
środki ramion) dzieli długość na pół − co łatwo udowodnić z tw. Talesa.
c.n.d.
11 lut 00:15
Dlaczemu nie?: hmm blisko bylem. Ja porównałem pole trójkąta do pola trapezu no i niestety wyszło
ba+b co
nie bardzo się sprawdza bo żeby dowód był prawdziwy a musiałoby być równe b... Dzięki
11 lut 00:27