Analiza matematyczna egzamin poprawkowy ryan: Nie mam pojęcia o tych zadaniach, a niestety termin ostatniej możliwej poprawki egzaminu się zbliża, mam nadzieję, że ktoś nie tylko podsunie mi odpowiedzi do zadań ale również spróbowałby podpowiedzieć lub odesłać w miejsce gdzie mógłbym taką pomoc odnaleźć. Mamy trochę na to czasu bo do piątku. Jeśli ktoś się podejmie rozwiązania chociaż części proszę o kontakt. Chciałbym zaznaczyć, że niestety początkowo mogę okazać się z tego całkowicie zielony. 1. Oblicz granice ciagów przy n dążacym do nieskończonosci a) lim ( √4n2+5n−7−2n) b) lim (n−7/n)ⁿ

	4n5+2n4−3n+8
c) lim
	3n5−2n3+81

d) lim (2n−√4n²+2n)

	5n3−3n2+7
e) lim (		)
	3n4−5n+1

f) lim (2n⁶−5n⁴+7n³+8)

	6x4+8x+7
g) lim
	2x3−4x+5

h) lim (2n− √4n²+2n

	7n4−3n2+9
i) lim
	3n4−5n+1

2.Oblicz granice funkcji (x dążące do 0 )

	5x4+4x3−5
a) lim
	6x3−2x2+8

	sin7x
b) lim
	2x

	x−sinx
c) lim
	x3

	sin4x
d) lim
	6x

3. Wyznacz przedziały monotoniczności i ekstrema funkcji

	x2
a) f(x)=
	x2−16

	x2
b) f(x)=		− myślę ze jeden można uznać za przykład i wtedy sam będę mógł
	x2−9

spróbować zrobić ten podpunkt c)y=x²*e^−x d)y=(x²−3)*e^x

	x2−3
e)y=
	x−2

4. Oblicz pochodne funkcji a) y=e^4x3−5x2+7 b) y=ln √2x+3 c) y=(2x⁴+7x²+15)³ d) y=ln(2x²−4x+1) e) y=e {^2x+9_3x−5} f) y+arctg√2x+1

	2x−5
g) ln
	5x2+4

h) y=e^5x2−7x+8 i) y=x^cosx j) y=ln √8x−5 5.Wyznacz asymptopy wykresu funkcji

	x3
a)f(x)=
	x2−4

b) y= U{4x²}{5x−10

	3x2
c)y=
	2x+4

	2x2−5
d) f(x)=
	x2−4

Oo: Czas poświęcony na przepisywanie tego tutaj można było poświęcić na przeglądanie notatek z ćwiczeń czy wykładów (o ile chodziłeś na zajęcia i notowałeś).. tym bardziej że łatwiejszych zadań z 1 semestru już nie mogłeś dostać...

Oo: Prawie wszystkie oprócz zad 3 i 5 można rozwiązać w pamięci. Wystarczy minimalna wiedza

ryan: niestety kolego Oo moja pamięc tego nie potrafi. Dosyć szybko udało mi się to przepisać. Mieliśmy praktycznie tylko ćwiczenia, niestety nie było za dużo godzin a i wykładowca się nie spisywał.

Oo: Jeśli ciąg ma w liczniku wielomian tego samego stopnia, co wielomian w mianowniku, to granicą jest iloraz współczynników przy najwyższych potęgach. Na przykład

	x2−6		1
lim		=
	3x2+54352		3

n−>∞

	sinx
lim		=1
	x

x−>0 na przykład

	sin(100x)
lim		=5
	20x

x−>0 granica ciągu, gdy n−>∞ i w liczniku jest wielomian stopnia wyższego, niż stopień wielomianu w mianowniku − wtedy granica wynosi ∞. analogicznie jeśli w mianowniku jest wyższy stopień wielomianu niż w liczniku, to granica wynosi 0. Banalnych przykładów jest o wiele więcej, ale − tak jak powiedziałam − trzeba było chodzić na ćwiczenia. Co do asymptot − jest wiele przykładów na tym forum, głównie liczenie granic. Monotoniczność i ekstrema − to samo, ale pochodne. Dziś rozwiązywałam wiele przykładów, wystarczy poszukać. Wzory na pochodne i wieeeeeeeeeeele rozwiązanych przykładów znajdziesz tutaj https://matematykaszkolna.pl/strona/359.html https://matematykaszkolna.pl/strona/360.html Jeśli pozwolisz komuś rozwiązywać zadania za Ciebie, to dalej nic nie będziesz potrafił. A jeśli nie potrafisz rozwiązać tak prostych przykładów, to przykro mi, ale inżynier nie dla Ciebie. Zrób sobie technika. Pozdrawiam i powodzenia

ryan: myślę, jednak że ktoś jeszcze mi kilka rad odnośne tych zadań podrzuci

Oo: Do którego konkretnie?

ryan: zadanie 3 i 5.

Artur z miasta Neptuna: 3. procedura wygląda tak: − wyznaczasz dziedzinę funkcji − obliczasz pochodną funkcji − przyrównujesz pochodną do zera (f'=0) − robisz szkic wykresu pochodnej (kiedy jest większa a kiedy mniejsza od zera) − jeżeli f'<0 to f↘, jeżeli f'>0 to f↗ − jeżeli dla jakiegos 'x' (np. x=1) f' = 0 i wykres pochodnej zmienia znak (z plusa na minus lub minusa na plus) to masz ekstremum zresztą poczytaj: https://matematykaszkolna.pl/strona/381.html https://matematykaszkolna.pl/strona/387.html

ryan: a mógłbyś dla przykładu chociaż po jednym przykladzie z tych zadań zrobić ?

Artur z miasta Neptuna: 5. − wyznaczasz dziedzinę funkcji − dla punktów z poza dziedziny (np. D_f = R/{2}) obliczasz granice lewo i prawostronną: lim_x−>2⁻ f(x) i lim_x−>2⁺ f(x) jeżeli chociaż jedna z tych granic będzie wynosić ⁺/₋∞ to jest w tym punkcie asymptota pionowa 'x=2' − obliczasz granice w + i − ∞ dla f(x), jeżeli żadna z nich nie wyjdzie ⁺/₋∞ to masz asymptoty poziome y = 'to co wyjdzie z danej granicy' −−− uwaga − granice mogą się różnić − jeżeli jedna z tych granic jest ⁺/₋∞ to dla niej liczysz asymptotę ukośną − jeżeli obie z tych granic są równe ⁺/₋∞ to dla obu liczysz asymptotę ukośną − asymptotę ukośną liczysz następująco:

	f(x)
limx−>+∞		= ..... i to co wyjdzie to '= a' (tak samo dla x−>−∞)
	x

a następnie liczysz lim_x−>+∞ f(x) − ax = .... i to co wyjdzie = b (tam samo dla x−>−∞) wynikiem będzie asymptota ukośna o równaniu y=ax+b (gdzie 'a' masz z pierwszej granicy, a 'b' z drugiej [po podstawieniu wyliczonego 'a']) jeżeli a lub b = ⁺/₋∞ to nie istnieje asymptota ukośna dla danej części wykresu (czyli w +∞ lub − ∞ lub w obu)

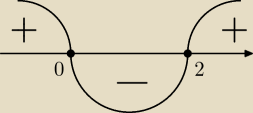
Artur z miasta Neptuna: 3. c) y=x²*e^−x D_f = R f' = 2xe^−x − x²e^−x = e^−xx(x−2) f'=0 ⇔ x = 0 ⋁ x−2 = 0 (pamiętaj e^{do każdej potęgi} > 0) ze szkicu odczytuję: f↘ w (0,2) f↗ w (−∞,0), w (2,+∞) x=0 jest ekstremum lokalnym (maksimum) x=2 jest ekstremum lokalnym (minimum)

Artur z miasta Neptuna: 5. d)

	2x2−5
f(x) =
	x2−4

	2x2−5
f(x) =		=> Df = R/{−2,2}
	(x−2)(x+2)

	−1
limx−>−2− f(x) = [		] = −∞
	0+

	−1
limx−>−2+ f(x) = [		] = +∞
	0−

	−1
limx−>2− f(x) = [		] = +∞
	0−

	−1
limx−>2+ f(x) = [		] = −∞
	0*

funkcja posiada asymptoty pionowe obustronne dane wzorami: x=−2 oraz x=2 lim_x−>−∞ f(x) = 2 lim_x−>+∞ f(x) = 2 funkcja posiada asymptotę poziome obustronną daną wzorem: y=2 do innych przykładów −−− w każdym z nich będziesz musiał wyliczać asymptoty ukośne

Artur z miasta Neptuna: jeżeli coś nie jest jasne ... to pytaj innych życzę miłego warunku z matmy albo zmiany studiów (w zależności za ile punktów ECTS masz matmę). nie zwalaj na wykładowcę ... studia nie są od tego, aby wykładowca się użalał nad wami, tylko byście WY się uczyli.

Trivial: e^iπ = −1 < 0.

macintos: w sumie to takie zadania i mi tez by sie przydały

Artur z miasta Neptuna: Trivial −−− nie wyjeżdżaj z zespolonymi, gdy człek pierwszego semestru nie zaliczy ale masz rację poprawiam się: ∀_x∊R e^x >0

ryan: o czym wy teraz mówicie to nie mam zielonego pojęcia