Funkcja wykładnicza- równanie i nierównośći wykładnicze V.Abel: Proszę o narysowanie i wytlumaczenie zbiorów na płaszczyźnie: A={(x,y)∊R² : 2^|x|≤16 i 3^|y−1|≤9} B={(x,y)∊R² : 2^{|x| + |y|}≤8}

WTF: 2^|x| ≤ 2⁴ => |x| ≤ 4 i 3^|y−1| ≤ 3² => |y−1| ≤ 2 A={(x, y)∊R²: |x| ≤ 4 i |y−1| ≤ 2 A={(x, y)∊R²: x ≤ 4 ⋀ x ≥ −4i y ≤ 3 ⋀ y ≥ −1 Drugi przykład zrób podobniem tylko tutaj musisz na przedziałach, czyli x≥0 i y≥0 V x≤0 i y≤0 V x≥0 i y≤0 V x≤0 i y≥0

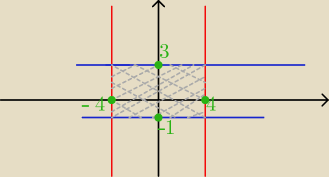
pigor: dla zbioru A : 2^|x|≤16 i 3^|{y−1|}≤9 ⇔ 2^|x|≤ 2⁴ i 3^|y−1|≤ 3² ⇔ |x|≤ 4 i |y−1|≤ 2 ⇔ −4 ≤ x ≤ 4 i −2 ≤ y−1 ≤ 2 /+1 ⇔ −4 ≤ x ≤ 4 i −1 ≤ y ≤ 3− szukany zbiór punktów (x,y) wewnątrz i na brzegu takiego prostokąta płaszczyzny R² dla zbioru B analogicznie, to zbiór punktów opisanych nierównością : |x|+|y|≤ 3 − wnętrze ograniczone rombem wraz z nim o środku w (0,0) i wierzchołkach w (−3,0) , (0,3) , (3,0) , (0,−3) . ...