.
elpe: dwie wysokości trójkąta ABC gdzie a=(−2;−3) zawarte sa w prostych o równaniach x−2=0 i
2x+3y−1=0 Oblicz współrzędne pozostałych wierzchołków tego trójkąta
ana:
2x+3y−1=0
3y=−2x+1
y=−2/3x+1/3 (pomarańczowa)
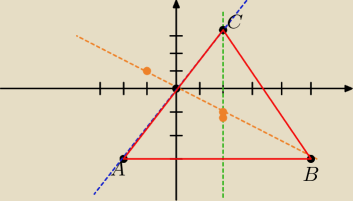
skoro prosta x=2 ma być wysokością szukanego trójkąta to wierzchołek B musi leżeć na prostej
y=−2/3x+1/3 i prostej y=−3:
−3=−2/3x+1/3
−9=−2x+1
2x=10
x=5
B=(5,−3)
punkt C z kolei napewno musi leżeć na prostej x=2 oraz na prostej prostopadłej do prostej
y=−2/3x+1/3 i przechodzącej przez punkt A
y−y
A=a(x−x
A)
a=3/2
y+3=3/2(x+2)
y=3/2x (niebieska)
czyli C=(2,3)
 2x+3y−1=0
3y=−2x+1
y=−2/3x+1/3 (pomarańczowa)
skoro prosta x=2 ma być wysokością szukanego trójkąta to wierzchołek B musi leżeć na prostej
y=−2/3x+1/3 i prostej y=−3:
−3=−2/3x+1/3
−9=−2x+1
2x=10
x=5
B=(5,−3)
punkt C z kolei napewno musi leżeć na prostej x=2 oraz na prostej prostopadłej do prostej
y=−2/3x+1/3 i przechodzącej przez punkt A
y−yA=a(x−xA)
a=3/2
y+3=3/2(x+2)
y=3/2x (niebieska)
czyli C=(2,3)
2x+3y−1=0
3y=−2x+1
y=−2/3x+1/3 (pomarańczowa)
skoro prosta x=2 ma być wysokością szukanego trójkąta to wierzchołek B musi leżeć na prostej
y=−2/3x+1/3 i prostej y=−3:
−3=−2/3x+1/3
−9=−2x+1
2x=10
x=5
B=(5,−3)
punkt C z kolei napewno musi leżeć na prostej x=2 oraz na prostej prostopadłej do prostej
y=−2/3x+1/3 i przechodzącej przez punkt A
y−yA=a(x−xA)
a=3/2
y+3=3/2(x+2)
y=3/2x (niebieska)
czyli C=(2,3)