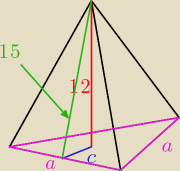Oblicz objętość ostrosłupa prawidłowego trójkątnego To_Tylko_Ja: Oblicz objętość ostrosłupa prawidłowego trójkątnego, którego wysokość jest równa 12 cm, a wysokość ściany bocznej 15 cm. Jak to zrobić ?

Kejt: 15²−12²=c² 225−144=c² c²=81 c=9

	1
c=		h
	3

	1
9=		h
	3

h=27

	a√3
h=
	2

	a√3
27=
	2

a=...

	a2√3
Pp=
	4

dalej sobie poradzisz..?

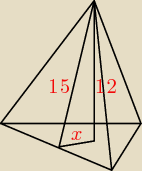WTF: Potrzebny nam jest bok trójkąta, czyli krawędź podstawy, która jest trójkątem równobocznym. Liczymy: 12²+ x² = 15² 144 + x² = 225 x² = 81 x = 9

	1		2
Z własności podziału wysokości na odcinki		i		zauważamy, że:
	3		3

	1
x =		hp, gdzie hp − wysokość podstawy
	3

	1		a√3
x =		*
	3		2

	a√3
x =
	6

	a√3
9 =
	6

54 = a√3

	54√3
a =
	3

a = 18√3 Zatem objętość to:

	1
V =		*Pp*H
	3

	1		(18√3)2√3
V =		*		*12
	3		4

V = 972[j³]

kas: 12²+x²=15² x=9 jest to 1/3 wysokości podstawy czyli cała h_p = 27

a√3
	=27
2

	54
a=
	√3

	a2√3
V=1/3 *Pp*h=1/3*		*h=972√3
	4

WTF: A tak zapomniałem dopisać tego '√3' Objętość to : 972√3 cm³

mańka173: Podstawą ostrosłupa jest prostokąt o bokach 6 cm i 8 cm. Oblicz objętość tego ostrosłupa, jeżeli każda jego krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze 60 stopni.

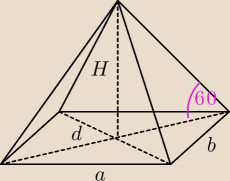dero2005: a = 8 b = 6 d = √a² + b² = 10

H
	= tg 60o = √3
d2

H = 5√3

	a*b*H
V =		= 32√3
	3