podobieństwo trójkątów m: Mam trapez równoramienny, gdzie a=21, b=9, c=10. Jak z podobieństwa obliczyć długości odcinków powstałe po przecięciu się przekątnych? Powstają właśnie 2 tr. podobne.

Artur z miasta Neptuna:

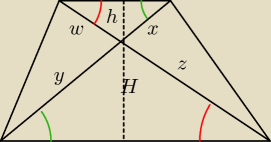
	y		z		H
kolory pokazują, które kąty są jednakowe, więc		=		=
	x		w		h

nie wiem jakie jeszcze masz dane (czy to co podałeś to jest 'wszystko')

m: Jeszcze h trapezu 8 i przekątne po 17 cm, ale Twoim sposobem chyba nie policzę.

m: a może być x/y=9/21 i x+y=17?

Artur z miasta Neptuna: no to masz, że:

	21
y= x*		oraz x+y = 17 −−−−> rozwiązujesz układ (wstawiasz 'y' do drugiego równania i
	9

wyliczasz 'x')

m: @Artur Zrobiłem tak, ale czy to na pewno jest poprawnie?

Artur z miasta Neptuna: jak najbardziej dla przykładu −−− narysuj jakiś prostokąt i sprawdź (prostokąt to szczególny przypadek trapezu równoramiennego).

m: Niestety nie mam tyle czasu, bo zaraz muszę się zbierać, ale zrobię tak jak właśnie chciałem. Dzięki Artur.

Żak: Masz złotowłosa koślawą optykę(coś ty namalowała−trapez ma być równoramienny),za dużo danych c(?) i złośliwie chachmęcisz ?=^a_b i zmień pseudo na to telewizyjne(bądź z wariatkowa)

m: Żak nie hejtuj tylko potwierdź, bo potrzebuję tego dobrze.