Dlugosci bokow trojkata wynosza 6,8,10. Oblicz promien okregu opisanego na tym t Meggi: Dlugosci bokow trojkata wynosza 6,8,10. Oblicz promien okregu opisanego na tym trojkacie i promien okregu wpisanego w ten trojkąt.

Aga1: Zauważ, że jest to trójkąt prostokątny o przeciwprostokątnej c=10, przyprostokątnych a=6, b=8

	1
R=		c −−−promień okręgu opisanego na trójkącie prostokątnym
	2

	a+b−c
r=		promień okręgu wpisanego w trójkąt prostokątny
	2

Podstaw i oblicz.

kubi:

Mariusz: Gdybyś chciał do tego podejść ogólnie to wyjdź z wzoru na pole trójkąta to z sinusem

	1
P=		absinγ
	2

a następnie skorzystaj z twierdzenia sinusów

c
	=2R
sinγ

c=2Rsinγ

	c
sinγ =
	2R

	ab		c
P=		*
	2		2R

	abc
P=
	4R

Mając dane długości wszystkich boków możesz policzyć pole powierzchni trójkąta chociażby ze wzoru Herona a następnie wstawić do powyższego wzoru

Mariusz: Co do promienia okręgu wpisanego to jeśli ten trójkąt podzielisz na trzy mniejsze trójkąty to możesz zauważyć że promień okręgu wpisanego będzie wysokością każdego z tych trójkątów natomiast podstawami tych trójkątów będą kolejne boki wyjściowego trójkąta Stąd dostaniesz wzór na pole powierzchni trójkąta o danych długościach boków i promieniu okręgu wpisanego w trójkąt

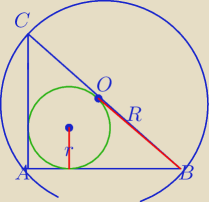
Mila: ΔABC− Δprostokątny 1) R=5 2) P_Δ=24 P_Δ=p*r

	6+8+10
p=		=12
	2

24=12*r r=2