Ekstrema i monotonicznosc serte: Zbadaj ekstrema lokalne i monotoniczność f(x)=^{2x + 1} _{x − 4} Dziedzina wychodzi R/{4} Pochodna wychodzi ⁻⁹_x²−8x+16, D_f'=D_f. Co dalej? Bo jesli robie f'(x)>0 → wychodzi −9 > 0 ? Co robie źle?

morlok:

−9
	≥0 dla x∊R\{4} bo iloraz liczby ujemnej i liczby zawsze dodatniej daje liczbę
(x−4)2

ujemną. Pochodna jest zawsze ujemna więc funkcja malejąca dla x∊R\{4}. Jeśli funkcja jest monotoniczna, to nie ma ekstrema

Aga1:

2(x−4)−(2x+1)		−9
	=
(x−4)2		(x−4)2

Pochodna nie ma miejsc zerowych, więc nie istnieje ekstremum −9(x−4)²<0 dla x∊R−{4} funkcja jest malejąca (−∞,4) oraz (4,∞)

morlok: Narysuj wykres funkcji wymiernej i wszystko zobaczysz

	2x+1		2(x−4)+9		9
f(x)=		=		=2+
	x−4		x−4		x−4

morlok: Aga1 wydaje mi się, że funkcja może mieć ekstrema lokalne jednocześnie nie mając miejsc zerowych ;>

morlok: Achh przepraszam Aga1, nawet dobrze nie spojrzałem. To jest pochodna, a nie wykres tej funkcji

Aga1: A jaki jest warunek konieczny istnienia ekstremum? morlok zwróć uwagę, że funkcja na całej dziedzinie nie jest malejąca, tylko przedziałami.

serte: Czyli funkcja nie jest nigdzie rosnaca? jest ciagle malejaca? chce to zrozumiec bez rysowania wykresow wlasnie

Aga1: Jest tylko malejąca, ale w przedziałach, bo 4∉D

morlok: Kilka niedociągnięć pisania na szybko. Wyżej pomyliłem znaki. Pochodna jest ≤0 a nie większa. I napisałem, że jest ona ujemna dla x∊R\{4}. Funkcja jest malejąca wtedy gdy pochodna jest malejąca. Zatem nasza funkcja maleje dla x∊R\{4}, dla x=4 nie jest określona. Aga1 napisałem, że źle przeczytałem. Myślałem, że chodzi Ci o miejsca zerowe funkcji, a nie pochodnej. Poprawiłem się. Co do funkcji malejącej to napisałem, że na całej dziedzinie oprócz x=4.

morlok: Jest różnica między "funkcja malejąca na x∊R\{4}" a "funkcja malejąca na x∊(−∞,4)∪(4,∞)"?

serte: Ok, dzieki A sprawdzisz teraz to ? : (polecenie to samo) f(x) = ^x₂ + ²_x D_f = R − {0} f'(x) = ¹₂ − ²_x² D_f'=D_f f'(x) = 0 <=> ^{x2 − 4}_2x² > = 0 <=> x₁ = 2, x₂= −2 Zatem funkcja rosnaca dla x ∊ (−∞, 2) u (2, ∞) funkcja malejaca dla x ∊ (−2, 0) u (0, ∞) ekstrema : wychodza mi dwa minimum lokalne, fmin1 = (2,2), fmin2 = (−2,−2)

serte: poprawka, tam mialo byc funkcja malejaca dla x ∊ (−2, 0) u (0, 2)

morlok: Wszystko ok ; )

morlok: Tylko (−2;2) to max

morlok: Bleee znów z rozpędu, (−2;−2) max

Aga1: Pochodna i miejsce zerowe pochodnej policzone dobrze, a dalej są błędy. Mnie uczono,że przy monotoniczności przedziały oddziela się przecinkiem. Jest minimum i maksimum. Spróbuję to rozrysować.

morlok: Nie ma żadnych błędów, tylko ten 1 błąd z maksimum lokalnym zamiast minimum ; p a tak to wszystko jest ok, nie słuchaj jej ; d

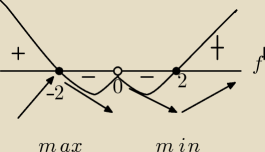
Aga1: y_max=f(−2)=−2 y_min=f(2)=2

morlok: Jeśli mam być upierdliwy tak jak Aga, to rysunek ma niedokładny bo z rysunku wynika, że y_max=f(−1) a y_min=f(1) już nie mówiąc, że w przedziałach (−2,0) i (0,2) funkcja maleje i rośnie

morlok: aaale głupoty piszę matko.. ale i tak rysunek źle, nic sie nie da odczytać. już lepiej tabelką

morlok: z rysunku y_min=f(−1)

Aga1: morlok nie mam ochoty z Tobą polemizować. Wyraziłam swoje zdanie i koniec tematu.

morlok: Czepiasz się rzeczy, które są dobre i źle narysowałaś chłopakowi wykres funkcji, do tego nie potrafisz odpowiedzieć na pytanie.. Dobrze, że wolisz nie brać się za polemizowanie. serte, coś jeszcze?

serte: Oki, następny przykład do sprawdzenia (jesli mozecie ) : f(x)= ^{x2 + x −1}_{x² − x + 1} D_f = R f'(x) = ^{−2x2 + 4x}_{x² − x + 1²} D_f' = D_f f'(x) = 0 <=> ^{−2x2 + 4x}_{x² − x + 1} = 0 <=> x₁ = 0, x₂ = 2 zatem funkcja rosnaca dla x ∊(0,2) funkcja malejąca dla x ∊ (−∞, 0) u (2,∞) fmin = (0, −1), fmax = (2, ⁵₃)

serte: coś te ułamki rozjechały się mam nadzieje, ze czytelne

morlok: Zamiast małej literki u używaj wielkiej U jak robisz kreskę ułamkową wszystko ok

serte: Kolejny przykład :

	x
f(x) = √
	2−x

Chcialem spytać czy dobrze wyliczlem dziedzine i przejdę dalej D_f : x ∊ <0, 2) u (2, ∞) ?

morlok: Dziedzina

	x
x≠2 i		≥0 ⇔ x(2−x)≥0 ⇔ x∊<0,2)
	2−x

serte: Tak tak, rozumiem, zapomnialem ze liczb ujemnych nie pierwiastkujemy. Teraz mam problem z wyznaczeniem pochodnej, wychodzi jakis kosmos, inaczej niz na wolframie

morlok: Dziedzina funkcji własnymi słowami są to takie liczby x (argumenty), które możemy podstawić. Tobie dziedziną wyszły liczby x∊<0,2)∪(2,∞). W tym przedziale jest na przykład liczba 4. Sprawdzimy, czy możemy podstawić x=4.

	4
f(4)=√		=√−2. Nie istnieje pierwiastek z liczby −2 więc to znak, że dziedzina wyszła
	2−4

Ci źle ; )

morlok: To dawaj tą pochodną, zaraz ją obalimy

serte: Kurde, źle przykład napisałem, chodziło mi o :

	x
f(x) = x √		, dziedzina się zmieni na (0, 2)? czy zostanie ta sama?
	2−x

morlok: Pozostanie taka sama. A chodzi o pochodną tej funkcji? Już liczę

morlok: Taka sama treść zadania? Wyznacz monotoniczność i ekstrema?

serte: tak