proszę o rozwiązanie Kaśśśś: dany jest ciąg o wyrazie ogólnym an =2n+3 . Liczba wyrazów tego ciągu mniejszych od 50 jest równa

Artur z miasta Neptuna: 2n+3 < 50 => wylicz n

kret: Rozwiąż nierówność: 2n + 3 < 50, n∊N₊

Kaśśśś: 23,5 dobrze

Jolanta: nie, wyrazy ciagu mozesz sobie wyobrazić jako ludzi stojących w szeregu,kazdy ma numer na plecach to jest a_n.Miejsce w kolejce to n(ten jest drugi ten piąty)nie moze byc miejsce ułamkiem

Kaśśśś: więc mam zaokrąglić do 24 ?

Jolanta: nie 2*24+3=51 a to nie jest <50 23

Artur z miasta Neptuna: Kaśś wyszło Ci n<23.5 skoro 'n' ma być liczbą NATURALNĄ to jakie jest największe 'n' spełniające ten warunek? oczywiście n=23

Kaśśśś: ok rozumiem a poradzisz coś na ciąg geometryczny ? liczby {1}{4} , x ,{1}{2} tworzą rosnący ciąg geometryczny . liczba x wynosi

Artur z miasta Neptuna: a₁ = a₁ a₂ = a₁*q a₃ = a₁*q²

	a3
q2 =		=> wylicz q i podstaw do wzoru na a2
	a1

Jolanta: znasz własnośc ciagu geometrycznego ,dotyczy wyrazu środkowego a₁ a₂ a₃ a₃²=a₁*a₂

Jolanta: aj oczywiscie miało być a₂²=a₁*a₃

Kaśśśś: dzięki

Kaśśśś: Może umiecie to zrobić ? dla kata ostrego alfa spełniony jest warunek tg alfa = pierwiastek z jedenastu przez pięc ile wynosi cosinus ?

Artur z miasta Neptuna:

sin α		√11		√11
	= tgα =		⇔ sin α =		cosα
cos α		5		5

natomiast z jedynki trygonometrycznej masz, że: sin² α + cos²α = 1 −−− podstaw za sin²α to co wyżej (podniesione oczywiście do ²) i wylicz cos α

kret:

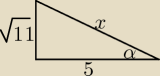
	5
x = √11 + 25 = 6, cosα =		i już
	6

Kaśśśś: wyszło mi sześć piatych ?

Kaśśśś: aha

Kaśśśś: mam wykazać że liczba pierwiastek z trzech − dwa pierwiastki z dwóch − pierwiastek z dwóch = jest całkowita Jak