pytanie egzaminacyjne
tomek: Mam takie pytanie Czy pochodna funkcji f(x)=|x| istnieje w punkcie x=1?
6 lut 18:39
tomek: albo czy jeżeli f'(x) istnieje w przedziale (−1;1), to f(x) jest ciągła w punkcie 0.
7 lut 09:04
Artur z miasta Neptuna:
1) funkcja jest różniczkowalna w punkcie x
0 gdy, granice lewo i prawostronna postaci:
są sobie równe.
2) funkcja jest ciągła w punkcie x
0, gdy granice lewo i prawostronna postaci:
lim
x−>x0 f(x)
są sobie równe.
pochodna f(x)=|x| w punkcie x
0=1 istnieje (w punkcie x
0=0 nie istnieje).
drugi wpis jest błędny −−− f'(x) NIE istnieje na całym przedziale (−1,1) −−− lub jak wolisz ...
funkcja f(x) nie jest różniczkowalna na całym przedziale (−1,1).
7 lut 09:31
Artur z miasta Neptuna:
3. Jeżeli funkcja f jest różniczkowalna na pewnym przedziale (a,b) to jest ona ciągła na tymże
przedziale.
7 lut 09:34
tomek: a różniczkowalna tzn że ma pochodna?
7 lut 09:46
Artur z miasta Neptuna:
funkcja jest różniczkowalna = funkcja posiada pochodną
7 lut 09:48
tomek: oki wielkie dzieki

7 lut 09:49
tomek: A jeszcze jedno pytanie czy każda suma całkowa jest nie ujemna

7 lut 10:03
tomek: wynikiem całki oznaczonej jest zawsze liczba dodatnia

7 lut 10:04
Artur z miasta Neptuna:
niee

przykład:
1
| | x2 | | 1 | | 4 | | 3 | |
∫x dx = [ |
| ]−21 = [ |
| − |
| ] = − |
| |
| | 2 | | 2 | | 2 | | 2 | |
−2
7 lut 10:07
tomek: czyli nie każda suma całkowa jest nieujemna? Całki dodatnie tyczą się tylko zastosowania całek?
7 lut 10:09
Artur z miasta Neptuna:
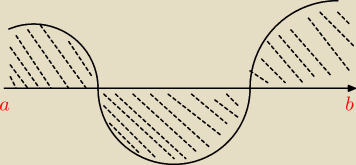
pole powierzchni krzywej, która jest PONIŻEJ osi OX jest liczona z minusem

rysunek przedstawia jakie pole będzie liczyła całka oznaczona na przedziale (a,b)
7 lut 10:10
Artur z miasta Neptuna:
dlatego też bardzo często trzeba brać ∫ |f(x)| dx
7 lut 10:10
tomek:
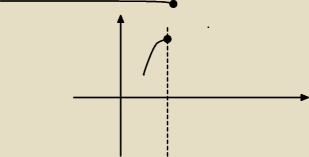
czy tak jak na rysunku jest pokazane to też jest maksimum lokalne? Bo mam pytanie czy jeżeli
funkcja f(x) ma maksimum lokalne, to nie istnieje funkcja odwrotna do niej.
A wiem też że żeby funkcja mogła być odwrotna to musi być różnowartościowa.
7 lut 10:21
tomek: to u góry powinno być po prawej stronie
7 lut 10:22
Artur z miasta Neptuna:
narysuj jeszcze raz ... i zaznacz, które kółko jest 'zapełnione' a które 'puste'
7 lut 10:25
tomek:
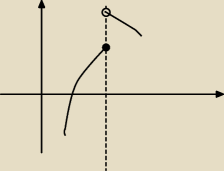
7 lut 10:28
Artur z miasta Neptuna:
trzeba wyróżnić parę przypadków:
1. funkcja nie jest ciągła (czyli także nie jest różniczkowalna) na całym przedziale (a,b)
wtedy może istnieć funkcja f−1 pomimo, że funkcja f(x) posiada maksimum/minimum lokalne (a
nawet globalne), dla której Df−1 = ZBf
2. funkcja jest ciągła (ale nie musi być różniczkowalna) na całym przedziale (a,b) => jeżeli
funkcja posiada minimum/maksimum lokalne to nie jest to funkcja różnowartościowa => nie
istnieje f−1 dla funkcji f(x) z dziedziną zawierającą odcinek (a,b).
7 lut 10:30
Artur z miasta Neptuna:
dana funkcja nie posiada maksimum lokalnego (dąży do niego, ale go nie osiąga) ... nie jest ona
różniczkowalna w przedziale (a,b), ale posiada funkcję odwrotną.
7 lut 10:31
tomek: czyli skoro ma maksimum lokalne to nie istnieje funkcja do niej odwrotna?
7 lut 10:36
Jack:
tak, ponieważ nie będzie różnowartościowa.
7 lut 10:39
Artur z miasta Neptuna:
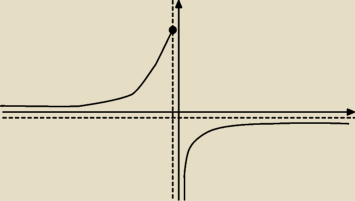
a niby dlaczego nie?
podany przykład to trochę zmodyfikowany wykres hiperboli (obciąłem go w x=−1, aby uzyskać
maksimum lokalne, a nawet maksimum globalne)
| | 1 | |
jak wiesz, wykres takiej hiperboli to f(x) = − |
| Df = R/{0} i posiada ów funkcja f−1 = |
| | x | |
Moja modyfikacja polega na tym, że masz:
| | 1 | |
f(x) = − |
| Df = R/(−1,0). |
| | x | |
tak funkcja posiada funkcję odwrotną:
| | 1 | |
f−1 = − |
| Df−1 = (−∞,0) ∪ (0,1> |
| | x | |
7 lut 10:42
Artur z miasta Neptuna:
więc tak ... jeżeli dziedzina funkcji jest R i f jest ciągła to jak najbardziej masz rację −−−
maksimum/minimum lokalne oznacza, że funkcja nie posiada odwrotnej (ponieważ f(x) nie jest
różnowartościowa).
Jednak to nie dotyczy funkcji, które nie są ciągłe na R lub ich dziedzina ≠ R
7 lut 10:44
tomek: | | 1 | |
no ale pochodna |
| nigdy nie równa sie 0 to jak to się wyjaśnia? |
| | x | |
7 lut 10:50
Artur z miasta Neptuna:
Funkcja nie posiada maksimum/minimum lokalnego tylko i wyłącznie w punktach w których f' = 0
przykład: f(x) = |x| (minimum dla x
0 = 0, natomiast w tym punkcie nie jest ona
różniczkowalna/nie posiada pochodnej − patrz. warunek na istnienie pochodnej) −−− jest to
klasyczny przykład obrazujący, że zerowanie się pochodnej w punkcie x
0 nie jest jedynym
przypadkiem dla którego funkcja posiada ekstremum w jakimś punkcie swojej dziedziny
Po prostu to co wcześniej narysowałem ... tam dla x
0 = −1 pochodna NIE ISTNIEJE

7 lut 11:02



 przykład:
1
przykład:
1
 pole powierzchni krzywej, która jest PONIŻEJ osi OX jest liczona z minusem
pole powierzchni krzywej, która jest PONIŻEJ osi OX jest liczona z minusem  rysunek przedstawia jakie pole będzie liczyła całka oznaczona na przedziale (a,b)
rysunek przedstawia jakie pole będzie liczyła całka oznaczona na przedziale (a,b)
 czy tak jak na rysunku jest pokazane to też jest maksimum lokalne? Bo mam pytanie czy jeżeli
funkcja f(x) ma maksimum lokalne, to nie istnieje funkcja odwrotna do niej.
A wiem też że żeby funkcja mogła być odwrotna to musi być różnowartościowa.
czy tak jak na rysunku jest pokazane to też jest maksimum lokalne? Bo mam pytanie czy jeżeli
funkcja f(x) ma maksimum lokalne, to nie istnieje funkcja odwrotna do niej.
A wiem też że żeby funkcja mogła być odwrotna to musi być różnowartościowa.

 a niby dlaczego nie?
podany przykład to trochę zmodyfikowany wykres hiperboli (obciąłem go w x=−1, aby uzyskać
maksimum lokalne, a nawet maksimum globalne)
a niby dlaczego nie?
podany przykład to trochę zmodyfikowany wykres hiperboli (obciąłem go w x=−1, aby uzyskać
maksimum lokalne, a nawet maksimum globalne)
