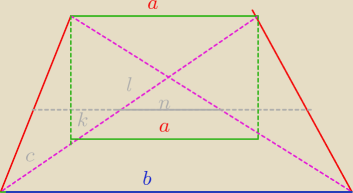
trapez - odcinek laczacy przekatne trapezu jok: Wykaż,że odcinek łączący środki przekątnych trapezu jest równoległy do jego podstaw i ma długość

a−b
2

l		k+l
	=
n		a

la= nk + nl la−ln = nk l(a−n) = nk

	nk
l=
	a−n

l		c+k+l
	=
n		b

lb − nl = nc + nk l(b−n) = nc +nk

	nc+nk
l=
	b−n

	nk
l=
	a−n

nk		nc+nk
	=
a−n		b−n

bkn − n²k = anc + ank − n²c − n²k < podziele wszystko /n bk − nk = ac + ak − nc − nk bk − ak = ac − nc

k(b−a) −ac
	= −n
c

Jak udowodnic to tym sposobem? nie wychodzi

jok: ktoś chetny do pomocy?

jok: podbijam:z bo musze wiedziec

Godzio: Musisz mieć akurat tym sposobem ?

jok: https://matematykaszkolna.pl/forum/30872.html < tutaj mam Twoj ale chyba ten jest dla mnie prostszy, chyba ze sie tak nie da.

Godzio: Czy da ? Trudno mi to określić, na pewni jest duuuużo motania

jok: Jezeli jest duzo motania, to chociaz napisz gdzie robie błąd.

Godzio: Naczy to nie chodzi nawet o błąd, mogą być duże problemy z odpowiednimi przekształceniami Ale zobaczę czy jest ok

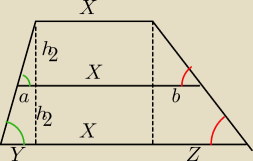
Artur z miasta Neptuna: suma podstaw = X + X + Y + Z = 2X + Y + Z trójkąty po lewej są do siebie podobne (te same kąty) ... tak samo trójkąty po prawej

	a		Y		b		Z
korzystasz z tw. Talesa (		=		i		=		)
	h/2		h		h/2		h

i Ci ładnie pięknie wychodzi

Artur z miasta Neptuna: i macie gotowy dowód tegoż twierdzenia dla DOWOLNEGO trapezu

Godzio: Błędu nie ma, moment się zastanowię, jak to pociągnąć do końca

Artur z miasta Neptuna: ajjj ..... sorki ... pomyliłem Twierdzenia już robię do tego zadania dowód

jok: Dzieki artur, to i Godzia z wyzej podanego linka rozumiem, chce znac 3 sposoby.

jok: jakies postepy? u mnie nic nie idzie

jok: jezeli dam ze k=l, to 2n =a, a = b−c

	b−c
wtedy n=
	2

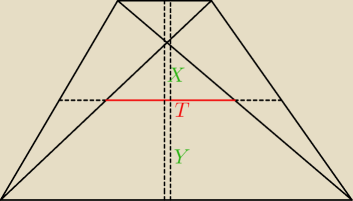
Artur z miasta Neptuna: 1. przekątne tworzą trójkąty podobne (te same kąty)

	a		y+x
2. wysokości tych trójkątów trzymają proporcję		=
	b		y−x

	h
3. y =		<− łatwo wykazać
	2

	y+x
a = b*
	y−x

	y+x		2x		a−b		x
a−b = b* (		−1) = b* (		) =>		= b*
	y−x		y−x		2		y−x

natomiast z tw. Talesa wiemy, że:

T		x		x		a−b
	=		=> T = b*		=
b		y−x		y−x		2

c.k.d

Artur z miasta Neptuna: w razie pytań − wal śmiało

jok: dzieki

jok: dlaczego y−x?

Artur z miasta Neptuna: y−x to jest wysokość mniejszego trójkąta i wynika z tego, że ta wysokość + x = h/2 = y

jok: ok, reszte KUMAM, dzieki

Mila: Patrz rysunek Artura

	a+b
Cały odcinek w którym zawiera sięT ma długość
	2

	b
Każdy "przerywany odcinek" ma długość
	2

	a+b		a−b
czerwony odcinek:		−b =
	2		2