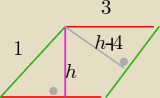
planimetria - rownoleglobok jok: 13.Długosci boków równoległoboku pozostają w stosunku 1:3 . Wyznacz wysokości tego rónolegloboku wiedzac ze jedna jest o 4 cm krótsza od drugiej. Oblicz wysokosci

1		3
	=
h		h+4

3h = h + 4 h=2 odp h₁ = 2, h₂ = 6 prawidlowa odpowiedz h₁ = 2, h₂ = 4 Gdzies jest bląd?

Kejt: skoro jedna wysokość ma być krótsza od drugiej o 4 cm to na pewno nie mogą być one równe 2 i 4..

Eta: odp: h₁= 2 h₂=6 jest prawidłowa P= 3*h₁ = 1*h₂ = 6

Kejt: ale wg powinno to wyglądać tak: boki: a;b

a		1
	=
b		3

b=3a a*(h+4)=bh a(h+4)=3ah h+4=3h −2h=−4 h=2

Aga1: Boki a= x, b=3x x*(h+4)=3xh//:x h=2

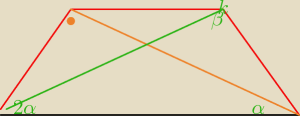
jok: dzieki 1)wykaż, że jeśli w trapezie równoramiennym krótsza podstawa i ramię mają taką samą długość, to przekątna trapezu zawiera się w dwusiecznej kąta ostrego tego trapezu. Tego nie rozumiem Rysunek do 2 zadania 2)Wykaz ze jesli przekatna trapezu rownoramiennego jest dwusieczna kata ostrego i tworzy z drugim ramieniem kat prosty to kat ostry trapezu jest rowny 60^o β= 90 + α 6α = 180 2α=60

Eta: 2/ 2α+α= 90^o ⇒ α= 30^o to 2α= 60^o

jok: a pierwsze zadanie?

Aga1: Na pierwszym rysunku masz uzasadnienie 1) pierwszy zaznaczony kąt α,to kąt między niebieskim a zielonym bokiem, drugi kąt (prawy górny) też α, bo to są kąty odpowiadające, a więc równe. Trzeci kąt po lewej stronie między zielonym a czerwonym bokiem też α, bo trójkąt o bokach b,b jest równoramienny i kąty przy podstawie(zielonej) ma równe. Przekątna zielona dzieli kąt ostry trapezu na dwie równe części, więc jest dwusieczną tego kąta.