.
Kasia: Dane:
P(A') = 0,91
P(A∩B) = 0,01
P(A∪B) = 0,21
Szukane :
P(B)
P(B−(A∩B)
P((A∪B) − (A∩B))
wyliczylam P(B) korzystajac z wlasnosci P(A∪B) = P(A) + P(B) − P(A∩B)
ale nie wiem jak dalej wyliczyc, bo podobno nie mozna tak po prostu odejmowac tylko trzeba to
zamienic jakos na sume, a tego kompletnie nie lapie. Prosze bardzo o wytlumaczenie

4 lut 21:58
Kasia: ponawiam
4 lut 22:03
Mila: P(B−(A∩B))=P(B)−P(A∩B)
4 lut 22:07
Kasia: tez tak chcialam zrobic, jednak moja nauczycielka wyraznie zaznaczyla przy tlumaczeniu tego, ze
jest ZABRONIONE odejmowanie.. mimo,ze dla mnie to jest dobrze, jednak wedlug nie trzeba
koniecznie nastepowac na sume konbinujac jakos.. więc juz nic z tego nie rozumiem.
Mozna normalnie odejmowac

tak samo co do tego trzeciego przypadku, mozna odjac po prostu
P(A∪B) − P(A∩B)


4 lut 22:11
Kasia: hmmm?
4 lut 22:22
Mila: Najlepiej narysuj te zbiory i traktuj prawdopodobieństwo jak obliczanie pola.
4 lut 22:25
Artur z miasta Neptuna:
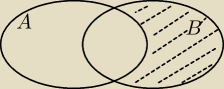
Bo może jej chodzi o wykorzystanie tylko tego co było dane + ich dopełnień
P(B−(A∩B)) = P(A') − P((A∪B)')
4 lut 22:26
Kasia: tzn? bo jakoś za bardzo mi to nie wyjaśnia

ogólnie można zawsze odejmować czy faktycznie coś
jest nie tak z tym, i nie zawsze jest to 'dozwolone'?
4 lut 22:27
Kasia: no pewnie tak, dlatego pytam, czy odejmowanie jest jak najbardziej dozwolne czy nie? bo jeśli
tak, to widocznie faktycznie chce nas zmusic do większego zastanowienia się i do
pokombinowania, tylko moim zdaniem nie ma co mówić, że NIE WOLNO, tylko po prostu wystarczylo
powiedziec, ze mozna, ale chciałabym żebyscie zrobili tak i tak.. eh to szkolne nauczanie..
4 lut 22:29
Kasia: Arturze, czy możesz mi wyjaśnić moją wątpliwość

4 lut 22:34
Mila: Ja myślę, że Twojej Nauczycielce chodzi o rozpisanie na sumy zbiorów rozłącznych.
(A∪B)−(A∩B)=(A−B) ∪(B−A)=
4 lut 22:43
Kasia: ok, rozumiem Mila że chodzi o tego typu kombinacje, ale ponawiam moje pytanie : czy można po
prostu odjąc od siebie te zbiory

4 lut 22:45
Mila: P(B−(A∩B))= P(B−A)=P(B)−P(A∩B)
4 lut 22:46
Mila: Nie zawsze. Popatrz co Ci napisałam.
4 lut 22:47
Mila: Rysuj zbiory.Wtedy zobaczysz czy możesz skorzystać z aksjomatu o prawdopodobieństwie sumy
zbiorów rozłącznych.
4 lut 22:49
Kasia: nie rozumiem za bardzo wytlumaczenie dlaczego P(B−A) to to samo co P(B) − P(A∩B)
a takie inne pytanko mam jeszcze
jak mam wyliczyc to (A−B) to wtedy moge to rozpisac jako P(A) − P(B) czy nie? tak odnoszac sie
chocby do tego wczesniejszego przykladu, ktory rozpisalas w ten sposob.
4 lut 22:52
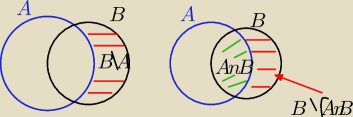
Mila:
A−B to elementy , które należą do A a nie należą do B.I nie możesz tak napisać .
P(A−B) =P(A) −P(A∩B)
Nie umiem rysować, ale A−B to to ta część zbioru A z zielonym.
4 lut 22:59
Eta:
4 lut 23:01
Kasia: aaaa

w taki sposób, okeej

to ja już szybciutko sprobuje rozwiazac ten 2 i 3 przyklad z
ktorym mialam problem i jesli mozesz to prosilabym bardzo o sprawdzenie, ok?

4 lut 23:02
Kasia: dzięki dziewczyny! rozumiem czym jest to B−A i A∩B, tylko zle jakos patrzylam na te koleczka i
coś mi się obzdurało, że mozna po prostu odjąc jeden od drugiego, co faktycznie nie wyszłoby.
Już rozwiązuję.
4 lut 23:04
Mila:
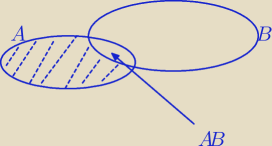
∩∩
4 lut 23:05
Eta:

4 lut 23:07
Kasia: ok, mam

mam nadzieję, że jest okej

P(B−(A∩B) = P(B) − P(A∩B) = 0,13 − 0,01 = 0,12
P((A∪B) − (A∩B)) = P(A−B) + P(B−A)
teraz tak na marginesie
P(A−B) = P(A) − P(A∩B)
P(B−A) = P(B) − P(A∩B)
powracając do wcześniejszego
P((A∪B) − (A∩B)) = P(A−B) + P(B−A) = P(A) − P(A∩B) + P(B) − P(A∩B) = 0,08 −0,01 + 0,13 − 0,01 =
0,08 + 0,12 = 0,2
4 lut 23:13
Kasia: moglibyście to sprawdzić czy jest poprawnie rozwiązane?

4 lut 23:19
Mila: No i teraz widzisz, że mogłaś od razu skorzystać z aksjomatu o rozłącznych zbiorach i obliczyć
to ostatnie

,21−0,01 = 0,2
Jak porobisz trochę tych zadań, to będziesz to rozumiała.
Gratuluję.
4 lut 23:22
Kasia: SUUUUPER!

Dziękuję bardzo Mila za pomoc

pozostałym również.
teraz widzę dlaczego nie zawsze można odejmować

4 lut 23:24

 tak samo co do tego trzeciego przypadku, mozna odjac po prostu
P(A∪B) − P(A∩B)
tak samo co do tego trzeciego przypadku, mozna odjac po prostu
P(A∪B) − P(A∩B) 

 Bo może jej chodzi o wykorzystanie tylko tego co było dane + ich dopełnień
P(B−(A∩B)) = P(A') − P((A∪B)')
Bo może jej chodzi o wykorzystanie tylko tego co było dane + ich dopełnień
P(B−(A∩B)) = P(A') − P((A∪B)')
 ogólnie można zawsze odejmować czy faktycznie coś
jest nie tak z tym, i nie zawsze jest to 'dozwolone'?
ogólnie można zawsze odejmować czy faktycznie coś
jest nie tak z tym, i nie zawsze jest to 'dozwolone'?


 A−B to elementy , które należą do A a nie należą do B.I nie możesz tak napisać .
P(A−B) =P(A) −P(A∩B)
Nie umiem rysować, ale A−B to to ta część zbioru A z zielonym.
A−B to elementy , które należą do A a nie należą do B.I nie możesz tak napisać .
P(A−B) =P(A) −P(A∩B)
Nie umiem rysować, ale A−B to to ta część zbioru A z zielonym.

 w taki sposób, okeej
w taki sposób, okeej  to ja już szybciutko sprobuje rozwiazac ten 2 i 3 przyklad z
ktorym mialam problem i jesli mozesz to prosilabym bardzo o sprawdzenie, ok?
to ja już szybciutko sprobuje rozwiazac ten 2 i 3 przyklad z
ktorym mialam problem i jesli mozesz to prosilabym bardzo o sprawdzenie, ok? 
 ∩∩
∩∩

 mam nadzieję, że jest okej
mam nadzieję, że jest okej  P(B−(A∩B) = P(B) − P(A∩B) = 0,13 − 0,01 = 0,12
P((A∪B) − (A∩B)) = P(A−B) + P(B−A)
teraz tak na marginesie
P(A−B) = P(A) − P(A∩B)
P(B−A) = P(B) − P(A∩B)
powracając do wcześniejszego
P((A∪B) − (A∩B)) = P(A−B) + P(B−A) = P(A) − P(A∩B) + P(B) − P(A∩B) = 0,08 −0,01 + 0,13 − 0,01 =
0,08 + 0,12 = 0,2
P(B−(A∩B) = P(B) − P(A∩B) = 0,13 − 0,01 = 0,12
P((A∪B) − (A∩B)) = P(A−B) + P(B−A)
teraz tak na marginesie
P(A−B) = P(A) − P(A∩B)
P(B−A) = P(B) − P(A∩B)
powracając do wcześniejszego
P((A∪B) − (A∩B)) = P(A−B) + P(B−A) = P(A) − P(A∩B) + P(B) − P(A∩B) = 0,08 −0,01 + 0,13 − 0,01 =
0,08 + 0,12 = 0,2

 ,21−0,01 = 0,2
Jak porobisz trochę tych zadań, to będziesz to rozumiała.
Gratuluję.
,21−0,01 = 0,2
Jak porobisz trochę tych zadań, to będziesz to rozumiała.
Gratuluję.
 Dziękuję bardzo Mila za pomoc
Dziękuję bardzo Mila za pomoc  pozostałym również.
teraz widzę dlaczego nie zawsze można odejmować
pozostałym również.
teraz widzę dlaczego nie zawsze można odejmować 