Przewiduję pokój :P ICSP: Trivial odpisz jak jesteś Chciałbym się czegoś nauczyć w końcu

Trivial: <:

Godzio:

ICSP: Dobrze O ile znowu Godzio się nie podszywa to byłbyś wstanie nauczyć mnie rozwiązywać równania zespolone?

Trivial: Ale je rozwiązuje się przecież dokładnie tak samo jak normalne. No nie? <:

ICSP: ale mi to kompletnie nie idzie Nigdy nie mam pomysłu jak się za to zabrać Chodzi mi o takie w których są sprężenia moduły itd.

Trivial: Sypnij może jakimś przykładem.

ICSP: z*|z| = 2ż gdzie ź to sprężenie

Trivial: Chyba najprościej podstawić z = x + iy i porównać części rzeczywiste i urojone.

ICSP: ale co zrobić z modułem ? przecież tam jest : √x² + y²

Trivial: no i?

Trivial: (x+iy)*√x²+y² = 2(x−iy) Rozdzielając:

⎧	x√x2+y2 = 2x
⎩	y√x2+y2 = −y

Trivial: −2y

ICSP: no i : (x+yi)√x²+y² = 2(x−yi) no i co z tym pierwiastkiem. Bo chyba nie do kwadratu

ICSP: aaa Teraz widzę

ICSP: x√x²+y² − 2x = 0 x(√x² + y² − 2) = 0 x = 0 v √x² + y² − 2 = 0 dla x = 0 otrzymujemy : y * |y| = −2y y * |y| + 2y = 0 y( |y| + 2) = 0 widać że tylko y = 0 spełnia to równanie. teraz drugi przypadek : √x² + y² − 2 = 0 √x² + y² = 2 y * 2 = −2y 2y = −2y y = 0 wstawiając do pierwszego otrzymamy x = 0 chyba się całkowicie pogubiłem

ICSP: chociaż y = 0 to x = √2 czyli mamy liczbę z = √2

ICSP: x = 2 *

Godzio: Hola, moi drodzy, takie rzeczy z postaci wykładniczej

ICSP: słucham

Trivial: Z drugiego równania wychodzi, że y = 0 lub √x²+y² = −2 ← nie zachodzi. Czyli y musi być 0. Wstawiamy do pierwszego x*√x²+y² = 2x x|x| = 2x x = 0 lub |x| = 2 Zatem równanie to spełniają punkty (0,0), (−2,0) oraz (2,0) Zatem z ∊ {−2,0,2}.

IQ: Trivial ty jesteś mózgiem możesz powiedzieć ile czasu spędzasz na naukę ?

Trivial: Podczas sesji całkiem sporo.

Godzio: z*|z| = 2ż z = re^iφ ź = re^−iφ |z| = r r²e^iφ = 2re^−iφ 1^o r = 0 Wiadomo 2^o r > 0 r² = 2r i φ = − φ + 2kπ r(r − 2) = 0 i φ = kπ r = 2 (r>0 więc r = 0 odrzucamy) i φ = 0, φ = π Zatem mamy: z₁ = 2(cos0 + isin0) = 2 z₂ = 2(cosπ + isinπ) = −2 z₃ = 0

ICSP: hmmm sprytne Myślę że już rozumiem o co w tym chodzi

IQ: @ICSP sory że tutaj A masz czasami tak że zapominasz rzeczy których się jakiś czas temu uczyłeś? Pytam bo widzę ludzie zarzucają zadania np z zespolonych, a ty to pewnie miałeś tylko na pierwszym roku, a mimo to wiesz jak rozwiązać

Godzio: Hehe, miałeś tylko na pierwszym roku

IQ: a nie ? Trivial chyba na matmie nie jest

ICSP: Godziu skąd znasz tą metodę Podoba mi się Możesz podać jakiś prosty przykład?

Trivial: Powiedzmy, że jeśli coś zrozumiałem (dobrze) to raczej pamiętam. A że staram się zrozumieć, a nie bezmyślnie kuć to zapamiętuję całkiem sporo.

Trivial: ICSP, to metoda przejścia na współrzędne biegunowe. Gdybyś studiował co innego to też byś już ją znał.

Godzio: Znam z wykładu z³ = (ź)³ z = re^iφ z³ = r³e^3iφ r³e^3iφ = r³e^−3iφ Pamiętamy zawsze o r = 0 2^o r > 0 r³ = r³ > 0 − r dowolne 3φ = −3φ + 2kπ

	π
φ =		* k
	3

k = 0 ⇒ ... k = 1 ⇒ ... k = 2 ⇒ ... k = 3 ⇒ ... k = 4 ⇒ ... k = 5 ⇒ ...

ICSP: hmm a są jeszcze jakieś inne ciekawe metody które można poznać ?

IQ: ja tą metodę też znałem ale zapomniałem pewnie właśnie dlatego że jej nie zrozumiałem a nauczyłęm się schematu. Dobra robie wyjazd

Godzio: Narazi ciekawych nie znam więcej

ICSP: hmm no dobrze Jeszcze jedno pytanie : Czy funkcje cyklometryczne są w liceum czy na studiach?

Godzio: studiach

ICSP: To jest sam początek analizy?

Trivial: Funkcje cyklometryczne są w przedszkolu.

ICSP: hmm Trivial do interesującego przedszkola chodziłeś

Trivial: Dobra powiem inaczej. Funkcje cyklometryczne wprowadzane są w ostatnich 15 minutach wykładu i uważa się, że od razu wiemy co i jak.

IQ: to teraz nie dziwie sie dlaczego tak wymiata my w przedszkolu nic nie robilismy

IQ: To co ty studiujesz?

ICSP: ale z analizy? Co mogę mieć w drugim semestrze na algebrze ? Czyżby to mogły być szeregi?

Godzio: O co do tego się zgodzę Dział "ciągłośćfunkcji" blablabla, funkcjami ciągłymi są także funkcje cyklometryczne jako odwrotne do trygonometrycznych I dziale "pochodne" wyprowadziliśmy sobie wzór na pochodną arcsinx jako funkcję odwrotną do sinx, korzystając z tw. o pochodnej funkcji odwrotnej

Trivial: IQ: informatykę. ICSP: nie wiem, przeczytaj sobie w sylabusie.

ICSP: Spoko Ja nawet nie wiem co to funkcja odwrotna xD Tzn wiem, ale nie miałem z tego żadnych ćwiczeń ani nic

Godzio: Bo to analiza

Trivial: Już widzę ICSP, który błaga o to, żeby mu wyjaśnić co to właściwie jest bijekcja, iniekcja i suriekcja za miesiąc.

ICSP: No to tylko czekać aż się ferie skończą Jeszcze tylko tydzień

Trivial: To Ty masz ferie już? Ja jeszcze do połowy sesji nie dobrnąłem. :<

ICSP: Trivial chyba za wcześniej niż miesiąc

IQ: skoro mówicie o funkcjach odwrotnych możecie mi powiedzieć co to jest sinh ?

ICSP: Ja już mam ferie od chyba 10 dni

Trivial: Tak. sinh = sh = sinus hiperboliczny. To jedna z tych funkcji które są wprowadzane w ostatnich pięciu minutach wykładu i są zupełnie bezużyteczne. Jeszcze z tego nie korzystałem, domyślam się, że można tym parametryzować punkty na hiperboli.

Godzio: Sinus hiperboliczny

Godzio: My mieliśmy tylko powiedziane (też przy ciągłości) że sh jest funkcją ciągłą, po czym na egzaminie otrzymujemy: ∫coshⁿxdx −− wyprowadzić wzór rekurencyjny

IQ: ok to super nie będe sie wgłębiać a tutaj jeszcze mi się pare pytań nasunęło jak chcecie możecie mnie dokształcić Czy ciągłość jest wystarczająca aby funkcja była różniczkowalna ?

Godzio: Nie zawsze, np: y = |x| nie jest różniczkowalne w zerze

Trivial: No to przecież trywialna całka jest. Łatwo zapamiętać wzory na funkcje hiperboliczne poprzez analogię do trygonometrycznych.

	eix+e−ix
cosx =
	2

	ex+e−x
coshx =
	2

Teraz to można sobie nawet wzór jawny wyprowadzić

Godzio: To wyprowadź Ale akurat miałem fuksa że się tego uczyłem, i to zadanie poszło bez problemu

IQ: ok dzięki Godzio A czy każdy ograniczony ciąg jest zbieżny ? Nie do końca rozumię to słowo zbieżny

Godzio: ∫coshⁿ⁻¹x(sinhx)'dx = coshⁿ⁻¹xsinhx − (n − 1)∫coshⁿ⁻²xsinh²xdx Później z jedynki trygonometrycznej i już praktycznie koniec

Godzio: Nie każdy ograniczony, ale każdy ograniczony z góry i rosnący, albo ograniczony z dołu i malejący jest zbieżny = posiada granicę

Godzio: Przykład ograniczonego i nie zbieżnego: a_n = (−1)ⁿ

IQ: ok kumam Czy funkcja jest ciągła w każdym odizolowanym punkcie d ? też tego odizolowany punkt nie rozumie

IQ: aaa

Godzio: Trudne pytanie Pierwsze słyszę

Godzio: wcześniej napisałem "jedynki trygonometrycznej" chodziło mi o hiperboliczną

IQ: Jeśli punkt należy do zbioru, ale nie jest jego punktem skupienia, to nazywamy go punktem izolowanym (tego zbioru). A zatem, punkt p należący do zbioru A jest izolowany wtedy i tylko wtedy, gdy istnieje takie jego otoczenie, które nie zawiera punktów zbioru A różnych od p.

Vizer: Odizolowany punkt to pewnie taki, gdzie mając funkcję, jest ona nagle przerwana(zaznaczona pustym kółeczkiem) a wartość dla tego argumentu jest gdzieś "wyrzucona", więc taka funkcja nie jest ciągła w tym punkcie. Przynajmniej ja to tak interpretuje, nie znając i nie spotykając się z definicją odizolowany punkt.

IQ: dobra ja nie wiem co to punkt skupienia jest

IQ: hmm to może być prawda co piszesz bo co innego

Trivial: Nie wiem czy jest sens wyprowadzać wzór jawny. Wyjdzie 'brzydki'.

Godzio: Punkty skupienia to takie punkty w których ciąg się skupia, przykładowo a_n = iⁿ (i − jednostka urojona) ma 4 punkty skupienia: −1,1,−i,i Ciąg który ma więcej niż jeden punkt skupienia nie jest zbieżny, i jeszcze mogę powiedzieć, że największy punkt skupienia to granica górna, a najmniejszy granica dolna ciągu

Godzio: No właśnie

IQ: kurde to są ważne rzeczy a mógłbyś podać jeszcze jeden przykład z punktem skupienia ?

Trivial:

	ex+e−x		1		n k
∫coshnxdx = ∫(		)ndx =		∫∑k=0...n		(ex)k(e−x)n−k dx =
	2		2n

	1		n k
=		∫∑k=0...n		e(2k−n)xdx =
	2n

	1		n k
=		∑k=0...n		e(2k−n)x + c
	2n		2k−n

Działa tylko dla przypadku, gdy n jest liczbą nieparzystą. Dla liczby n parzystej i przy

	n		n k
k=		wyraz tej sumy trzeba zastąpić wyrazem		x.
	2

Trivial: Jednak wyprowadziłem.

Godzio: Taki prosty to ten co podałem już: a_n = (−1)ⁿ −1 i 1

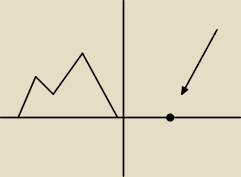
IQ: a ten punkt odizolowany to moze byc takie cos czyż nie ?

kazz: kazz