. Kasia: Witam proszę bardzo o pomoc z dwoma zadankami. 1. Student może odpowiedz na 30 pytan sposrod 45 zamieszczonych w zestawie egzaminacyjnym. Losuje cztery pytania. Jezeli odpowie na 4 pytania, otrzyma ocene bardzo dobra, jesli na 3 pytanoa − dobra, na 2 − dostateczna. Oblicz prawdopodobienstwo,ze : a) otrzyma ocene bardzo dobra b) otrzyma ocene co najmniej dostateczna 2. W urnie jest pewna liczba kul bialych i jedna kula czarna. Losujemy jedna kule z tej urny, zatrzymujemy ja, a nastepnie z pozostalych kul losujemy jedna kule. Ile powinno byc kul

	2
bialych w urnie, aby prawdopodobienstwo wylosowania dwoch kul bialych bylo rowne		?
	3

to drugie zadanie widze,ze chyba powinno byc zrobiona ta metoda z krzaczkiem, ktorego nienawidzę.. jesli mozna innym sposobem ( prostszym) zrobic, to proszę bardzo o wyjasnienie z gory dziekuje bardzo za pomoc : )

Artur z miasta Neptuna: 1.

	30*29*28*27
P(a) =
	45*44*43*42

	15*14*13*12		30*15*14*13
P(b) = 1 − (		+		)
	45*44*43*42		45*44*43*42

Kasia: nie potrzebuje rozwiazania tylko wyjasnienia..

Artur z miasta Neptuna: 2. A −−− wylosujemy w pierwszej białą i w drugiej białą B −−− wylosujemy w pierwszej czarną i w drugiej białą C −−− tego szukamy

	n*(n−1)
P(A) =
	(n+1)*n

	1*n
P(B) =
	(n+1)*n

	n2−n		n		n		2
P(C) = P(A) + P(B) =		+		=		=
	(n+1)*n		(n+1)*n		(n+1)		3

czyli n = 2

Kejt: o kurcze...wieki tego nie czytałam.. "nie potrzebuję rozwiązania, tylko wyjaśnienia" to aż dziwne..

Artur z miasta Neptuna: 1. a) −−− losuje 4 pytania na które zna odpowiedź ... czyli jedno z 30, później jedno z 29, jedno z 28 i jedno z 27 b) minimum dostateczną, czyli P(odpowiada na minimum 2 pytania) lub ... '1 − [P(nie odpowie na żadne) + P(odpowie tylko na 1)]

Kasia: no widzisz, jestem z tych, którzy lubią rozumieć to co mają do zrobienia.. kurcze, ale co do 2. to skąd wzial Ci sie ten wzor (n+1)*n ? pierwszy raz widze go na oczy przy zadaniach z prawdopobienstwa : ( a czy moglbys mi to rozrysowac tym drzewkiem? coś czuje, ze chyba musze sie polubic z ta metoda, bo z tym wzorem nic mi nie mowi..

Artur z miasta Neptuna: 2. inny sposób C' −−− wylosujemy w pierwszym białą, a w drugiej czarną (czyli przeciwieństwo tego co chcemy)

	n*1		n2		n		2
P(C) = 1 − P(C) = 1 −		=		=		=
	n*(n+1)		n*(n+1)		n+1		3

czyli n = 2

Artur z miasta Neptuna: n −−− ilość kul białych 1 −−− ilość czarnych n+1 −−− tyle kul przed pierwszym losowaniem n +1 − 1 = n −−−− tyle kul po pierwszym, a przed drugim losowaniem

Artur z miasta Neptuna:

	moc zdarzenia A
to nie jest żaden wzór ... wzór to P(A) =
	moc Ω

Kasia: ale skad Ci sie wzielo to,ze najpierw mnozyc 15 * 14, a w drugim przypadku 30*... itd.. nie rozumiem tego:(

Aga1: b)B^' otrzyma ocenę niedostateczną, jeśli nie odpowie na żadne pytanie lub odpowie na jedno

	30 0		30 1
IB'I=		+		=1+30=33

	42*43*44*45
IΩI=		=77*43*45
	24

	33
P(B)=1−P(B')=1−
	77*43*45

Sprawdź.

Aga1: Oj,źle zrobiłam, bo przecież losuje 4 pytania.

Artur z miasta Neptuna: masz 45 pytań .... na 30 umie ... na 15 nie umie jeżeli ma wylosować 4 pytania z których NA ŻADNE nie umie to musi wylosować jedno z 15, później jedno z 14, jedno z 13 i jedno z 12

	15 4
to jest chyba C154 =		... czy jakoś tak

Kasia: Aga, za pomocą wzoru Newtona 100 razy wole, jest jasno i przejrzyście, dzięki mozesz mi tylko powiedziec dlaczego ta moc omegi dzieli sie przez 24

Handball93: mam to gdzies w zeszycie robilem to nie dawno pozdrawiam 3 licealistke

Aga1:

	30 0		15 3		30 1		15 3
Poprawka IB'I=		*		+		*

Kasia: aaaa, kurde! nie zrozumialam polecenia to 'może odpowiec' to myslalam,ze taka mu daja mozliwosc, dlatego coś mi się nie zgadzalo... chwilka, sprobuje to rozpisac za pomoca Newtona ten przyklad a i sprawdzisz czy jest ok, dobra

Aga1:

	45 4		45!		42*43*44*45
IΩI=		=		=
			4!*41!		4!

4!=24

Kasia: teraz rozpisze jedynie IAI za pomoca wz. Newtona

	30 4
a) I A I =

	30 2		15 2		30 3		15 1		30 4
b) I A I =		*		+		*		+

tak?

	45 4
a czy Ω mozna zapisac tak : Ω =

Artur z miasta Neptuna: tak −−− dobrze

Aga1: Tak. B) można też krócej.

Artur z miasta Neptuna: wybacz, że ja tak nie rozpisuję, ale pierwsze czego się nauczyłem na prawdopodobieństwie ... to zapomnieć o tym "czy to jest kombinacja, wariancja czy inna permutacja"

Kasia: yeah to rozumiem wybacz Arturze, po prosto jakos mi łatwiej zapisywac i zrozumiec za pomoca wz. Newtona : ) a czy dalibyście rade rozpisac mi to 2 za pomocą drzewka? może wtedy mi się rozjasni

Kasia: ponawiam

Kasia: proszę pomózcie mi z tym drzewkiem:(

Artur z miasta Neptuna:

	1
A =
	n+1

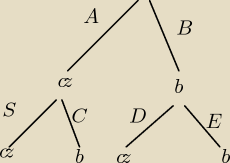
B = 1−A C = 1 (S = 1 − C = 0)

	1
D =
	n

E = 1−D cz −−− wylosowana czarna kula b −−− wylosowana biała kula UWAGA nie wiem czy lewa odnoga (opcja cz − cz) powinna być zaznaczona, gdyż ona nigdy nie zachodzi (jest tylko 1 czarna kula)

Kasia:

	1
czym jest tutaj n i skad Ci się wzielo to
	n+1

i co dalej ; p

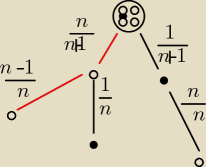
Aga1: n− liczba kul białych 1 kula czarna + −−−−−−−−−−−−−−−−− n+1 liczba wszystkich kul

n		n−1		2
	*		=
n+1		n		3

Kasia: hmm, musze chyba troche posiedziec nad tym i pomyslec skad sie wziely te poszczegolne mianowniki,ze tak je nazwe..

Kasia: chyba jednak za bardzo nie rozumiem tych ulamkow, moglby mi ktos troche wyjasnic skad sie one wziely wybaczcie, ale tego po prostu nie widze..

Aga1: Początek po lewej stronie wylosowano kulę białą : białych jest n wszystkich jest n+1

	n
Prawdopodobieństwo wylosowania jednej kuli białej wynosi
	n+1

Dalej lewa strona: jeśli wylosowaną białą kulę odłożymy, to zmniejszy się o 1 liczba kul białych i zostanie: n−1 , wszystkich będzie n−1+1=n

	n−1
Teraz prawdopodobieństwo wylosowania kuli białej wynosi
	n

Artur z miasta Neptuna: Aga −−− źle zrobiłaś ... bo cz−b też jest zdarzeniem sprzyjającym, a nie tylko losowani b−b

Artur z miasta Neptuna: sorki −− mój błąd

Aga1: Prawdopodobieństwo wylosowania dwóch kul białych , a nie przynajmniej jednej białej.

Kasia:

	1
a czemu po prawej na 1. galezce jest		jesli niby na jednej galazce suma ma wynosi 1?
	n+1

Aga1: Po prawej na pierwszej gałązce: wylosowano kulę czarną: ile jest kul czarnych ? JEDNA. A ile jest wszystkich na początku (czyli na pierwszych gałązkach od startu)? n+1.