Objętość i pole powierzchni ostrosłupa Dominik: W ostrosłupie prawidłowym czworokątnym suma długości wszystkich krawędzi jest równa 24cm.

	√2
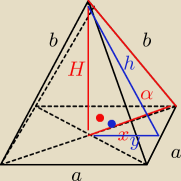
Krawędź boczna tworzy z postawą kąt, którego cosinus wynosi		. Oblicz objętość i pole
	4

tego ostrosłupa

Aga1: cosα=U{p2}}{4} 4a+4b=24 //:4 a+b=6⇒b=6−a

	a√2
x=
	2

	x
cosα=
	b

x=cosα*b rozwiąż wyliczając a i b Z twierdzenia Pitagorasa oblicz Hi jeszcze raz Pitagorasa obliczysz h.

hwdtel:

⎧	Pp=?=a2 + 2aH
⎜	H2=h2−(a2)2
⎨	4a+4h=24
⎩	√2a2h=√24

Dominik: Policzyłem a x= cosα*b

1		√2
	a√2=		*b
2		2

1		√2		√2
	a√2=		*(6−a) / :
2		2		2

1		√2
	a√2:		= 6−a
2		2

1		2
	a√2*		=6−a
2		√2

1		√2		√2
	a		*		= 6−a − pozbywam się pierwiastka z ułamka
2		√2		√2

1		2√2
	a		= 6−a / *2
2		2

	2√2
a		= 12−2a / +2a
	2

	2√2		2√2
a		+2a= 12 /
	2		2

	2√2
a+2a= 12:
	2

	2
3a= 12*
	2√2

	24		√2
3a=		*		− pozbywam się pierwiastka z ułamka
	2√2		√2

	24√2
3a=
	4

3a= 6√2 / :3 a= 2√2 b=6−a b= 6−2√2 − i teraz nie wiem jak to odjąć

Dominik: Przy pierwszym pozbywaniu się ułamka popełniłem błąd w zapisie powinno być tak

1		2		√2
	a		*		=6−a
2		√2		√2

I obliczyłem też b b=4√2 Dobrze?

Dominik:

	a√2		2√2*√2		4
Policzyłem też x=		=		=		=2
	2		2		2

Dominik: H²+x²=b² H²+2²=(4√2)² H²+4=32 H²=32−4 H²=28 H²=√28=√4*7=2√7

Dominik:

	1
y=		a
	2

	1
y=		*2√2=√2
	2

Aga1:

	√2
Dominik, popraw, bo cosα=
	4

a=2.

Dominik: poprowadziłem a=2 b=4 x=√2 y=1 H=√12 h=√15 Dobre wyniki mi wyszły?

Dominik: P_p=a² P_p=2²=4

	1
P=		*Pp*H
	3

	1
P=		*4*√14
	3

	4√14
P=
	3

Dominik: Zamiast "P" we wzorze ma być "V"

Dominik: P_c=P_p+P_b

	1
Pb=4*(		*2*√15)=4√15
	2

P_c=4+4√15

Aga1: H=√14