Izzac: Na płaszczyźnie zespolonej naszkicuj zbiór : A = { complex : |z² + 4| <= |z − 2i } Przyznam się że o ile wiem że druga część równania będzie okręgiem o środku w punkcie −2i, tak z pierwszą częścią nie wiem co zrobić

Godzio: |z − 2i| * |z + 2i| − |z − 2i| ≤ 0 |z − 2i|( |z + 2i| − 1 ) ≤ 0 |z − 2i| ≥ 0 zawsze, więc wystarczy rozpatrzyć: |z + 2i| ≥ 1 A tu mamy okrąg o środku (0,−2i) i promieniu 1 + wszystko na zewnątrz

Doniczka: jak sie moduły liczy w zespolonych ?

Doniczka: aha godzio jest mistrzem

Godzio: z = x + iy |z| = √x² + y²

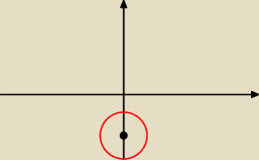
Muchomorek: Muszę zapytać jednak na wszelki wypadek taki będzie rysunek i zaznaczone wszystko poza powięrzchnią okręgu + jego obwód, tak?

Godzio: Powierzchnią koła jak coś Tak

Muchomorek: Mistrz xD

Muchomorek: A mam jeszcze jedno głupie pytanie, dlaczego tam odwraca się znak |z + 2i| ≥ 1 ?

Godzio: Dobrze, że na to zwróciłeś uwagę źle przepisałem Więc odpowiedź już będziesz znał