matematykaszkolna.pl
Planimetria ...: Potrzebny RYSUNEK Bok rombu ABCD ma dlugosć 5√5. Punkty M i N są środkami boków odpowiednio AB i AD. Proste zawierające odcinki BN oraz BM są prostopadle , a kąt DAB jest ostry. Oblicz pole rombu. Proszę o rysunek, bo nie wiem o co chodzi z tym, że "Proste zawierające odcinki BN oraz BM są prostopadle "
3 lut 17:30
...: pomoże ktoś? mi się wydaje, że taki kąt nie istnieje, może źle zaznaczam...
3 lut 17:42
Basiek : rysunek
3 lut 17:49
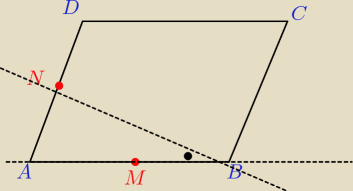
Basiek : Coś takiego ? Ten kąt prosty to wyszedł mi taki, że nic tylko zazdrościć....
3 lut 17:50
Artur z miasta Neptuna: taka konstrukcja nie jest możliwa ... jest błąd w zadaniu ... nie możliwe jest, aby NB⊥MB ∧ ABCD to romb
3 lut 17:51
...: No właśnie. Tylko, że to nie możliwe żeby tu było 90 stopni. Jak wielki by ten trapez nie był...
3 lut 17:53
Artur z miasta Neptuna: bo jeżeli AB zrobimy równolegle do ekranu/kartki (w poziomie), to aby BN ⊥ BM to BN musi być w pionie. W takim razie połowa boku AD musi być dłuższa niż bok AB −−−− sprzeczność bo |AB| = |AD| (dla rombu).
3 lut 17:53
Basiek : No właśnie widać, że to nie wyjdzie, bo rysunek jest w miarę poprawny, a kąta prostego tam nie będzie nigdy. Coś jest nie tak emotka
3 lut 17:54
Artur z miasta Neptuna: Rysunek poprawny poza kątem prostym ... Nie wiem skąd to zadanie ... ale jest ono błędnie podane −−− patrz mój dowód "na szybkiego".
3 lut 17:55
...: No czyli nie robię tego zadania. Jedno mniej Mam jeszcze problem z kilkoma zadaniami, ale żeby nie straszyć to wrzucę na razie tylko jedno emotka Przez punkt przecięcia się przekątnych trapezu ABCD o podstawach AB i CD poprowadzono prostą równoległą do BC przecinającą tę samą podstawę w punkcie R. Wykaż, że |AE|=|RB|
3 lut 17:57
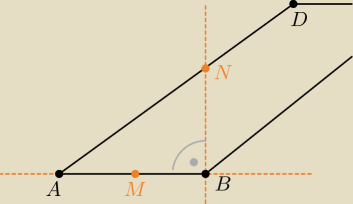
Artur z miasta Neptuna: rysunek Zrobisz ... w sensie pokażesz że jest to niemożliwe. Dowód −−− rysunek jak wyżej.
 |AD| |AB| 
Niech NB ⊥ MB i |AN| =
=
i |AB| = 5√5
 2 2 
|AN|2 = |AB|2+|BN|2
|AB|2 
= |AB|2 +|BN|2
4 
25*5 375 
= 25*5 + |BN|2 ⇔ |BN|2 = −
−−−− sprzeczne
4 4 
c.k.d.
3 lut 18:05
Basiek : Co znaczy skrót "c.k.d.", bo ciekawa jestem? :<
3 lut 18:10
Artur z miasta Neptuna: co kończy dowód
3 lut 18:11
Basiek : Dobra, oświeciło mnie "co kończy dowód"?
3 lut 18:11
...: Poproszę jeszcze o tak samo piękny dowód drugiego podyktowanego przeze mnie zadania
3 lut 18:20
...: Znajdzie się jakiś chętny by rozwiązać te o to piękne zadanie: Przez punkt przecięcia się przekątnych trapezu ABCD o podstawach AB i CD poprowadzono prostą równoległą do BC przecinającą tę samą podstawę w punkcie R. Wykaż, że |AE|=|RB|?
3 lut 18:32
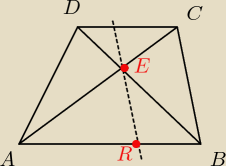
Artur z miasta Neptuna: rysunek Coś tu 'nie teges' Chyba, że punkt E to nie jest punkt przecięcia się przekątnych Poza tym, co oznacza stwierdzenie 'przecinającą tę samą podstawę' −−− tę samo co 'kto/co' ? Bok BC ? Bok BC nie przecina żadnej podstawy, a jeżeli nawet to przecinałby obie emotka Gołym okiem widać z rysunku, że dla takiego umieszczenia punktów |AE| ≠ |RB|
3 lut 18:40
...: Sorry, wcięło mi pól zadania... Całość brzmi tak: Przez punkt przecięcia się przekątnych trapezu ABCD o podstawach AB i CD poprowadzono prostą równoległą do AD, przecinającą podstawę AB w pkt. E oraz prostą równoległą do BC przecinającą tę samą podstawę w punkcie R. Wykaż, że |AE|=|RB|
6 lut 22:39
...: poszukuje chętnych
6 lut 22:56
...: może jutro znajdę emotka
6 lut 23:26
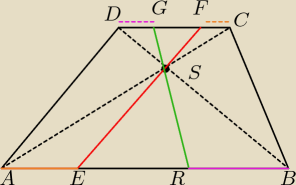
Artur z miasta Neptuna: rysunek aaaa ... no to inaczej to wygląda teraz emotka ... zadanko nie jest trudne, już pokazuję. Oznaczenia: h1 i h2 −−− wysokości trójkątów (odpowiednio) SDC i SAB (lub jak wolisz − odległości punktu S od danych podstaw trapezu) a, b −−− długości podstaw (odpowiednio) AB i CD a' = |AE| a'' = |RB Zauważasz, że: 1. ΔAES ∼ ΔCFS (te same kąty) 2. ΔBRS ∼ ΔDGS (te same kąty) 3. |AE| = |DF| ⋀ |RB| = |GC| korzystasz z 1 oraz 3.
|AE| |CF| |AE| b − |DF| |AE| b−|AE| 
=
⇔
=
⇔
=
⇔
h2 h1 h2 h1 h2 h1 
 a' b−a' h1 h1 
⇔
=
⇔ b−a' = a'
⇔ b = a'(1+
)
 h2 h1 h2 h2 
korzystasz z 2 oraz 3.
|RB| |DG| |RB| b − |GC| |RB| b−|RB| 
=
⇔
=
⇔
=
⇔
h2 h1 h2 h1 h2 h1 
 a'' b−a'' h1 h1 
⇔
=
⇔ b−a'' = a''
⇔ b = a''(1+
)
 h2 h1 h2 h2 
czyli:
 h1 h1 
a'(1+
) = b = a''(1+
)
 h2 h2 
 h1 h1 
a'(1+
) = a''(1+
)
 h2 h2 
a' = a'' C.N.W.
7 lut 09:25
Vax: Można trochę szybciej, (korzystam z rysunku wyżej) niech Q będzie punktem przecięcia AD i BC, wtedy trójkąty ABQ i ERS są jednokładne, niech X będzie środkiem tej jednokładności, wtedy X jest punktem przecięcia QS i AE (jednokładność przekształca S na Q i E na A) skąd X jest środkiem AB (wynika to szybko z Twierdzenia Cevy i Talesa) i z definicji jednokładności, jeżeli k jest skalą to XA = k*XE , XB = k*XR czyli k*XE = k*XR ⇔ XE = XR a stąd AE = RB cnd.
7 lut 17:49
...: dzięki za pomoc emotka Tak jak wcześniej wspomnialem mam jeszcze kilka zadań z którymi mam problem. O to jedno z nich: Z wierzchołka kąta rozwartego rombu opuszczono dwie prostopadle do jego boków. Długość każdej prostopadłej jest równa a, zaś odległość między spodkami tych prostopadłych jest równa b. Oblicz pole rombu. Jakieś strasznie skomplikowane obliczenia mi wychodzą gdy używam samych pitagorasów i tw. cosinusów. Przydałby się jakiś łatwiejszy sposób emotka
7 lut 21:47
...: to może dzisiaj ktoś?
8 lut 19:01
...: i?
8 lut 20:37
...: ghm, ghm
8 lut 21:22