ekstrema Karo: ekstrema

	1
f(x)= x2 +
	x2

dziedzina: D_f ∊ R \{0} obliczam pochodna

	2x4 −2
f'(x) =
	x3

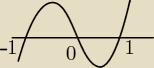
pochodna sie zeruje dla x = −1 i x = 1 i nie wiem co z 0 (nie nazlezy do dziedziny )? wykres znakow rysuje z prawej strony od góry i niechce mi wyjsc wykres bedzie przecinał 0 czy bedzie sie odbijal?

Karo: up

Krzysiek: 2x⁴ −2 =2(x⁴ −1) =2(x² −1)(x² +1)=2(x−1)(x+1)(x² +1) więc x=−1 min x=1 min

Karo: dlaczego przecina 0?

Artur z miasta Neptuna: wykres Krzyska super ale ... ale w 0 musi być zaznaczone 'o', że w tym punkcie pochodna nie przyjmuje wartości widać od razu, że w granice dla x→0⁻ oraz x→0⁺ wynoszą +∞

Krzysiek:

	2x4 −2
ponieważ:		zamieniasz na: (2x4 −2)x3 i rysujemy tzw. 'wężyk'
	x3

Krzysiek: no tak, Artek, ale ten punkt nam do niczego nie jest potrzebny więc tego nie zaznaczałem

Karo: ale dlaczego przecina 0 a nie odbija sie?

Krzysiek: ponieważ, potęga jest nieparzysta

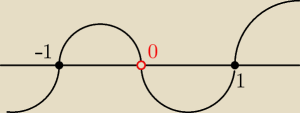
Artur z miasta Neptuna: nie nie ... Krzysiek mi chodzi o (rysunek) jeżeli się nie "wyłączy" 0 z pochodnej to szkic jest źle zrobiony = punkty trza "upitolić"

Krzysiek: szkic jak sama nazwa wskazuje to rysunek poglądowy, a nie wykres naszej funkcji, więc ja nie powiedziałbym, że szkic jest źle zrobiony bo interesuje nas znak pochodnej w innych punktach. Ale to też zależy jak kto się uczył.

Aga1: Musisz wiedzieć, gdzie pochodna przyjmuje wartości dodatnie , a gdzie ujemne, więc rozwiązujesz nierówność f^'>0 oraz f^'<0 i 0 musisz zaznaczyć , a w odpowiedzi uwzględniasz dziedzinę.