Zbadaj monotoniczność i ekstrema funkcji Korkitaczer: Zbadaj monotoniczość i ekstrema funkcji f(x)=x−ln(1+x)

Korkitaczer: Prosiłbym o pomoc w tym zadaniu.

Krzysiek: https://matematykaszkolna.pl/strona/i15.html

Korkitaczer: f(x)=x−ln(1+x) f'(x)=1−¹_1+x*(1+x)' f'(x)=^1+x_1+x−¹_1+x f'(x)=^x_1+x f'(x)=0⇔^x_1+x=0⇔1+x=0⇔x=−1 czyli wychodzi na to że funkcja ma maksimum w punkcie x=−1. dobrze zrobiłem ?

Krzysiek:

	x
nie..		=0 czyli x=0...
	x+1

mianownik musi być różny od zera.. aby sprawdzić czy to min czy max,

	x
rysujesz wykres		i badasz znak wokół punktu x=0
	1+x

https://matematykaszkolna.pl/strona/387.html

Korkitaczer: wykresem będzie prosta, czyli nie ma minimum ani maksimum tak ?

Krzysiek:

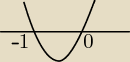
	x
nie,		zamieniasz na: x(1+x) , z założeniem, że x≠−1
	1+x

więc w punkcie 0 mamy min

Korkitaczer: aha, rozumiem. dziękuje za pomoc