maxima i minima funkcji tabelka z przedziałami rośnie maleje Bart: witam, mam problem z rozwiązaniem 2 przykładów a nigdzie nie mogę znaleźć analogicznych przykładów 1) f(x)=x⁴−8x² 2) f(x)=6x²−x⁴ dokładne polecenie to: określ przedziały w których funkcja "f" jest rosnąca lub malejąca, znajdź minima i maxima funkcji, naszkicuj wykres funkcji proszę pomóżcie mi i w miarę możliwości wytłumaczcie od a do z z góry dziękuję

Krzysiek: https://matematykaszkolna.pl/strona/381.html https://matematykaszkolna.pl/strona/387.html

Bart: dzięki Krzysiek próbowałem w ten sposób z tym walczyć i nie mam pojęcia co i jak tam wpisywać w 1 przykładzie dochodzę do momentu f(x)=x⁴−8x² f'(x)=4x³−16x f'(x)=4x(x²−4) f'(x)=4x(x−2)(x+2) no i z tego wychodzi mi 2 i −2 tyle że nie wiem co dalej z wzorów na minimum i maximum wychodzi mi maximum f(−2)=−8 minimum f(2)=−8 czy to jest dobrze i co dalej mam z tym zrobić?

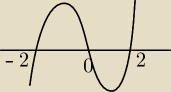
Krzysiek: więc w punkcie x=−2 funkcja przechodzi z minus w plus więc jest min dla x=0 plus w minus więc max x=2 jest min f' (x) > 0 −funkcja rosnąca, możesz z wykresu odczytać (wtedy gdy wykres jest nad osią ) podobnie kiedy malejąca

Bart: wielkie dzięki a jakbyś mi jeszcze powiedział skąd wiadomo, że akurat w −2 funkcja przechodzi z minus w plus wiem głupie pytanie ale już się w tym wszystkim gubię i czy to 0 tam wychodzi z tego, że przed nawiasami jest 4x

Krzysiek: funkcja w sensie wykres pochodnej funkcji. dla x=−2, pochodna na lewo jest pod osią czyli ujemna (czyli funkcja jest malejąca) , po prawej jest dodatnia(czyli funkcja jest rosnąca ) więc np. wyobrażasz sobie parabolę i funkcja maleje potem rośnie więc w tym punkcie jest minimum lokalne tak, zaznaczasz wszystkie miejsca zerowe pochodnej i rysujesz tzw. 'wężyk '

Bart: wielkie dzięki mam nadzieję rozbroję całą resztę i ogarnę to jakoś jeszcze raz dziękuję